Forschungsbericht 2019 - Max-Planck-Institut für Chemische Physik fester Stoffe
Direkte Abbildung von Orbitalen in Quantenmaterialien
Die Idee zur direkten Abbildung von Elektronenorbitalen ist angelehnt an existierende Techniken in der Absorptionsspektroskopie: Die spektrale Intensität eines dipolerlaubten Übergangs wie s→p hängt von der Orientierung des elektrischen Feldvektors des Photons relativ zur Orientierung des p-Orbitals ab. Würde man für alle Winkel des Polarisationsvektors messen, würde die gemessene Intensitätsverteilung direkt die Form des p-Orbitals widerspiegeln, da das kugelförmige s-Orbital des Anfangszustands nicht zur Richtungsabhängigkeit beiträgt. Wir möchten nun das gleiche für d- oder f-Orbitale machen, aber die Übergänge s→d oder s→f sind dipolverboten. Hier kommen die nicht-resonante unelastische Röntgenstreuung (NIXS), auch Röntgen-Raman genannt, und die neue Max-Planck-Messstation P01 an DESY/PETRA-III in Hamburg ins Spiel.
![Abb. 1: Projektion der dreidimensionalen orbitalen Form vom Nickelion im NiO Einkristall auf zwei Ebenen, eine durch [001] und [100] (a) und die andere durch [001] und [110] (b) definiert. Die Datenpunkte in den polaren Abbildungen (a) und (b) sind die integrierten Intensitäten der M1 (3s→3d)-Anregungen der Nickelionen im NiO. Die kleine Abbildung in (b) zeigt die theoretische orbitale Funktion (blaue gestrichelte Linie) und die für die Winkelauflösung des Analysators korrigierte Funktion (blaue durchgezogene Linie). Für (a) war diese Korrektur unerheblich. (c) dreidimensionale Lochverteilung der sogenannten high spin 3d8-Konfiguration im Nickelion.](/15016828/original-1625231899.jpg?t=eyJ3aWR0aCI6MjQ2LCJvYmpfaWQiOjE1MDE2ODI4fQ%3D%3D--cc4e089c4d857eea68468f4c32641f526a01e77c)
Abb. 1: Projektion der dreidimensionalen orbitalen Form vom Nickelion im NiO Einkristall auf zwei Ebenen, eine durch [001] und [100] (a) und die andere durch [001] und [110] (b) definiert. Die Datenpunkte in den polaren Abbildungen (a) und (b) sind die integrierten Intensitäten der M1 (3s→3d)-Anregungen der Nickelionen im NiO. Die kleine Abbildung in (b) zeigt die theoretische orbitale Funktion (blaue gestrichelte Linie) und die für die Winkelauflösung des Analysators korrigierte Funktion (blaue durchgezogene Linie). Für (a) war diese Korrektur unerheblich. (c) dreidimensionale Lochverteilung der sogenannten high spin 3d8-Konfiguration im Nickelion.
Für ein NIXS-Experiment sind sowohl Energie also auch Größe und Richtung des Impulsübertrags wichtig. Beide kann man durch die passende Streugeometrie und die Energie des einfallenden Röntgenstrahls wählen. Für kleine Impulsüberträge sind die Übergänge durch Dipol-Auswahlregeln bestimmt, und man erhält im Prinzip die gleiche Information wie in einem Röntgenabsorptionsexperiment. Der Unterschied ist, dass die Richtungsabhängigkeit des Impulsübertrags die Richtungsabhängigkeit des elektrischen Feldvektors übernimmt. Für große Impulsüberträge von etwa 10 Å-1 sind auch Nicht-Dipolübergänge erlaubt; sogenannten Multipolübergänge gewinnen Intensität. So werden dipolverbotene Übergänge wie 3s→3d (M1) der 3d-Übergangsmetalle sichtbar mit Intensitäten, die mehr als ausreichend für ein quantitatives Experiment sind. Da die Methode der orbitalen Abbildung auf Übergängen von einem s-Orbital basiert, nennen wir unsere Methode s-NIXS.
Wir haben die Machbarkeit der s-NIXS Methode an NiO getestet, dem Lehrbuchbeispiel für stark korrelierte antiferromagnetische Isolatoren. Dazu wurde die Energieabhängigkeit der Streuintensität der M1-Kante von Nickel in NiO für viele Kristallorientierungen gemessen und anschließend die integrierte Intensität in einer polaren Abbildung wie in Abb. 1a und 1b dargestellt. Man erkennt sofort, dass dies direkte Aufnahmen des Orbitals in der 3d-Elektronen-Loch-Verteilung von Nickel sind [1], wenn man es mit dem theoretisch berechneten, dem sogenannten high-spin 3d(x2-y2/3z2-r2). Zustand des Ni2+-Ions in oktaedrischer Symmetrie vergleicht (Abb. 1c). Die Ergebnisse in Abb. 1a und b erhält man ohne aufwendige Auswertungen. Das Auftragen integrierter Intensitäten reicht völlig aus. Wir glauben, dass dies das erst Mal ist, dass man im wahrsten Sinne des Wortes in der Lage ist, ein quantenmechanisches Objekt „zu sehen“, nämlich das atomare Orbital, was ja im Prinzip nichts anderes als ein rein mathematisches Konstrukt ist.
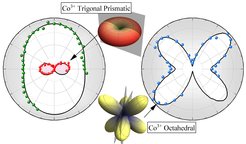
Abb. 2: Untersuchung des Oxids Co3Co2O6. Die Datenpunkte in den polaren Abbildungen sind die integrierten Intensitäten der M1 (3s→3d)-Anregungen in Cobalt. Die dreidimensionalen Darstellungen zeigen die für das Experiment relevanten Schnitte. Die blauen Punkte sind das Ergebnis für das Integral der oktaedrischen Co-Anregungen und stimmen sehr gut mit der gesamten Lochdichte (schwarze Linie) der sogenannten d6 low-spin Konfiguration überein. Die grünen Punkte sind das Ergebnis für das prismatische trigonale Co, sie stimmen sehr gut mit der berechneten Lochdichte der d6 high-spin Konfiguration (schwarze Linie) überein. Hier besetzt das sechste Elektron das d2-Orbital mit Donut-Form. Seine Abbildung erhält man, indem man die gemessene Lochdichte von der Lochdichte eines d5-Orbitalsabzieht. Die roten Punkte sind das Ergebnis.
Unsere s-NIXS-Methode haben wir anschließend auf Ca3Co2O6 angewendet. Dieses Oxid zeigt mit zunehmender magnetischer Feldstärke treppenähnliches Verhalten in der Magnetisierung, was auf Quantentunnel-Effekte hinweist. In vielen theoretischen und experimentellen Studien wurde versucht, die Eigenschaften von Ca3Co2O6 zu erklären. Darin sah es so aus, als wenn die besonderen Eigenschaften in dem ungewöhnlichen Arrangement der Atome begründet sind: Eindimensionale Ketten laufen entlang der c-Achse mit alternierenden CoO6-Oktaedern und trigonalen Prismen. Außerdem bilden diese Ketten in der ab-Ebene ein dreieckiges Prisma. Es scheint, dass die magnetischen Eigenschaften auf der geometrischen Frustration und dem Auftreten von Ising-Magnetismus basieren. Es ist jedoch nicht klar, woher der Ising-Magnetismus in diesem Material kommt. Alle Studien basieren auf Rechnungen mit mehr oder weniger widersprüchlichen Ergebnissen.
Abbildung 2 zeigt einen Schnappschuss vom Ergebnis unseres s-NIXS Experiments an der M1-Kante von Cobalt in Ca3Co2O6 [2]. Die orbitalen Abbildungen erlauben die eindeutige Zuordnung von Valenz, Spin und orbitalen Zuständen der beiden Umgebungen der Co-Ionen. Die oktaedrischen Co-Ionen zeigen eine sogenannten 3+ low spin t2g6 Konfiguration und die prismatischen trigonalen Co einen 3+ high-spin d6-Zustand , wobei das sechste Elektron das d2-Orbital besetzt. Dieses besitzt eine Donut-ähnliche Form. Dieses Orbital hat ein sehr großes orbitales Moment von 2mB und liefert damit eine natürliche Erklärung für den Ising-Magnetismus in Ca3Co2O6.
Es ist erstaunlich, dass eine solche orbitale Besetzung in einem Oxidmaterial stabil ist. Dies liegt an der ungewöhnlichen, prismatisch trigonalen Koordination. Allerdings würde auch eine solche Koordination nicht die Donut-Form garantieren. Feine Details im Wechselspiel von Kristallstruktur und den verschiedenen elektronischen Freiheitsgraden sind wichtig, die von der Theorie mangels erforderlicher Genauigkeit nicht erfasst werden. Die experimentelle Bestimmung der orbitalen Zustände ist daher ein wichtiger Schritt nach vorn für das Verständnis der magnetischen Eigenschaften von Ca3Co2O6.
![Abb. 1: Projektion der dreidimensionalen orbitalen Form vom Nickelion im NiO Einkristall auf zwei Ebenen, eine durch [001] und [100] (a) und die andere durch [001] und [110] (b) definiert. Die Datenpunkte in den polaren Abbildungen (a) und (b) sind die integrierten Intensitäten der M1 (3s→3d)-Anregungen der Nickelionen im NiO. Die kleine Abbildung in (b) zeigt die theoretische orbitale Funktion (blaue gestrichelte Linie) und die für die Winkelauflösung des Analysators korrigierte Funktion (blaue durchgezogene Linie). Für (a) war diese Korrektur unerheblich. (c) dreidimensionale Lochverteilung der sogenannten high spin 3d8-Konfiguration im Nickelion. Abb. 1: Projektion der dreidimensionalen orbitalen Form vom Nickelion im NiO Einkristall auf zwei Ebenen, eine durch [001] und [100] (a) und die andere durch [001] und [110] (b) definiert. Die Datenpunkte in den polaren Abbildungen (a) und (b) sind die integrierten Intensitäten der M1 (3s→3d)-Anregungen der Nickelionen im NiO. Die kleine Abbildung in (b) zeigt die theoretische orbitale Funktion (blaue gestrichelte Linie) und die für die Winkelauflösung des Analysators korrigierte Funktion (blaue durchgezogene Linie). Für (a) war diese Korrektur unerheblich. (c) dreidimensionale Lochverteilung der sogenannten high spin 3d8-Konfiguration im Nickelion.](/15016828/original-1625231899.jpg?t=eyJ3aWR0aCI6ODQ4LCJmaWxlX2V4dGVuc2lvbiI6ImpwZyIsIm9ial9pZCI6MTUwMTY4Mjh9--ac72aa6d953935da6da6cb167d8828cd34b546a1)












