Forschungsbericht 2019 - Max-Planck-Institut für Evolutionsbiologie
Mathematische Modelle für Lebenszyklen einfacher Organismen
Von einfachen zu komplexen Lebenszyklen
Von Einzellern nehmen wir oft an, dass sie ein relativ langweiliges Leben führen: Sie entstehen durch Zellteilung, sind dann den größten Teil ihres Lebens alleine und teilen sich irgendwann selbst, um Nachkommen zu erzeugen - kümmern sich aber ansonsten nicht weiter um den Nachwuchs. Während dieses Bild auf viele bekannte Bakterien zutrifft, gibt es aber auch andere einfache Organismen, die sich auf ganz andere Weise vermehren: Blaualgen (Cyanobakterien) formen lange Kolonien und teilen sich später wieder in kleinere Kolonien. Wäre es nicht sinnvoller, wenn sich diese Zellkolonien sofort teilen und sich somit keine Konkurrenz um Ressourcen zu machen?
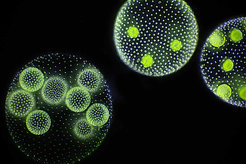
Bei der multizellulären Grünalge Volvox sehen die Zellen aus wie einzellige Grünalgen. Ihre Fortpflanzung ist jedoch völlig anders als bei echten Einzellern: Im Inneren der Mutterzelle werden gleich mehrere Kolonien von Tochterzellen gebildet, die beim Absterben der Mutterkolonie freigesetzt werden (Abb. 1). Wie kann solch ein komplexer Reproduktionsmechanismus entstehen? Wie kann er sich im evolutionären Wettbewerb gegen einen einzelligen Lebenszyklus durchsetzen, bei dem die einzelnen Zellen schneller eigene Nachkommen erzeugen? Diese Fragen stehen am Anfang unseres Verständnisses für die Evolution von komplexen Lebensformen.
Die Struktur von Zellpopulationen
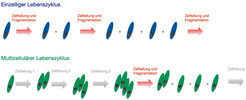
Man könnte nun versuchen, die faszinierende Vielfalt solcher Lebenszyklen anhand von immer neuen empirischen Beobachtungen zu erfassen und dann für jede Art experimentell analysieren, welche Biologie hinter dem Lebenszyklus steckt (Abb. 2). Als Theoretische Biologen wählen wir aber einen ganz anderen Ansatz: Wir untersuchen mathematisch, welche Lebenszyklen überhaupt optimal sein könnten. Denn nur, wenn ein neuer Lebenszyklus zu schnellerem Wachstum führt, kann er sich evolutionär durchsetzen. Dazu nehmen wir an, dass jede Konfiguration von Zellen durch eine Wachstums- und eine Sterberate charakterisiert ist: Ein Einzeller könnte mit höherer Wahrscheinlichkeit sterben als eine Einheit aus zehn Zellen, aber Zellen in einer größeren Einheit könnten es auch schwerer haben, Nährstoffe in der Umwelt aufzunehmen und damit langsamer wachsen. Der Lebenszyklus ist dann durch die Art und Weise, wie sich die Zellgruppe am Ende teilt, bestimmt. Natürlich sind diese Wachstums- und Sterberaten nicht unbedingt bekannt. Können wir auch ohne solche Informationen eine Aussage darüber machen, welche Art von Lebenszyklen zu maximalen Wachstumsraten führen kann? Das können wir, indem wir ein paar vereinfachende Annahmen machen, die die Evolution von Lebenszyklen auf demographische Modelle abbilden [1]. Wenn Gruppen von Zellen unabhängig voneinander sind, dann reicht es aus, über die Anzahl von Gruppen jeder Größe Buch zu führen. Nach einiger Zeit erreicht die Population ein demographisches Gleichgewicht, in dem sich der relative Anteil der einzelnen Gruppengrößen nicht mehr ändert und nur noch die Gesamtpopulation wächst.
Der evolutionäre Wettbewerb um die beste Reproduktionsstrategie
Weil jede Zellgruppe unabhängig ist, kann man die Dynamik eines solchen Systems durch ein lineares Gleichungssystem beschreiben. Die Populations-Wachstumsrate kann man nun aus diesen Gleichungen berechnen. Aber es reicht natürlich nicht aus, hier einfach eine Zahl anzugeben! Denn unser Ziel ist ja gerade, alle Lebenszyklen miteinander zu vergleichen, auch ohne Information über Details der Wachstums- und Sterberaten. Solch ein Vergleich ist möglich, wenn wir die mathematischen Eigenschaften dieses Gleichungssystems genau ansehen. Daraus ergeben sich gleich mehrere Aussagen:
(i) Für alle Wachstums- und Sterberaten gilt, dass der Lebenszyklus mit der maximalen Populations-Wachstumsrate deterministisch ist. Das bedeutet, dass eine Kolonie von Zellen immer zur gleichen Größe wächst und sich dann immer nach dem gleichen Muster teilt.
(ii) Die optimale Art, eine Kolonie von Zellen zu teilen, ist immer die Teilung in zwei Tochtergruppen. Das können zwei gleich große Gruppen sein, aber auch eine sehr große und eine sehr kleine Gruppe sein.
Hält sich die Biologie an solche Modelle?
Sind diese Aussagen nun „richtig'' in dem Sinne, dass sie die Biologie von einfachen mehrzelligen Lebensformen korrekt wiedergeben? Im Rahmen unserer Annahmen sind die Modelle natürlich richtig - vorausgesetzt, dass wir keine handwerklichen Fehler machen! Also müssen wir eine andere Frage stellen: Sind unsere Annahmen in der Biologie immer erfüllt? Diese Frage muss man natürlich verneinen, denn es gibt viele Organismen, die sich nicht in zwei Zellgruppen teilen, sondern in sehr viele Teile. Auch Volvox ist ein Beispiel dafür, dass unser obiges Modell noch nicht ausreichend komplex ist. Bisher haben wir nicht beachtet, dass sich die Umweltbedingen verändern können [2] und dass die Zellen der Mutterkolonie bei der Reproduktion verloren gehen. Das Zerbrechen des Zellverbandes ist also mit Kosten verbunden, da Zellen sterben. Wenn man aber solche Kosten berücksichtigt [3], dann sind weitere Lebenszyklen möglich, beispielsweise die Produktion von mehreren Nachkommen gleicher Größe. Das ist genau die Art eines Reproduktionsmechanismus, den man bei Volvox findet. Damit zeigt sich, dass man auf diesem Wege anhand von theoretischen Modellen untersuchen kann, welche Faktoren in der Biologie für die Evolution von Lebenszyklen wichtig sein könnten und nachfolgend die experimentelle Untersuchung dieser Faktoren anstoßen.













