Forschungsbericht 2021 - Max-Planck-Institut für Plasmaphysik
Effiziente Algorithmen für energiereiche Plasmateilchen

Magnetisch eingeschlossene, heiße Plasmen sind ein vielversprechender Weg zur Kernfusion und einer sauberen und klimaneutralen Energiequelle. Die im südfranzösischen Cadarache entstehende Großanlage ITER(siehe Link in der linken Spalte) soll Aufschluss über die technische Machbarkeit dieser Technologie geben. Ziel ist ein Netto-Energiegewinn. Es soll also mehr Energie freigesetzt als investiert werden. Dabei muss ein Teil der bei der Fusion frei werdenden Energie zur Heizung des Plasmas verwendet werden. Gelingt dies, spricht man von einem selbstständig brennenden Plasma. Hierin wechselwirken die energiereichen Fusionsprodukte – die bei der Verschmelzung von Deuterium und Tritium entstehenden zweifach positiv geladenen Helium-Kerne – mit dem umgebenden Plasma. Kommt es dabei zur Resonanz zwischen diesen energiereichen Teilchen und speziellen Alfvén-Wellen (Wellen im Plasma), kann dies den Fusionsprozess destabilisieren und die Selbstheizung des Plasmas stören
Simulation der Welle-Teilchen-Resonanz
Numerische Simulationen tragen zunehmend zum Verständnis dieser Welle-Teilchen-Resonanz in Fusionsplasmen bei. Die dabei benutzten Codes basieren meist auf sogenannten kinetischen Modellen. Sie eignen sich zwar hervorragend zur Beschreibung kollisionsarmer Plasmen, die weit vom thermischen Gleichgewicht entfernt sind, erfordern aber einen hohen numerischen Aufwand. Im Unterschied dazu werden Wellen im Plasma vornehmlich durch Fluidmodelle wie die Magneto-Hydrodynamik (MHD) beschrieben, die numerisch einfacher zu handhaben sind. Seit etwa drei Jahren verfolgt unsere Gruppe eine Hybridstrategie bei der Entwicklung numerischer Algorithmen, die Welle-Teilchen-Resonanzen simulieren: Der Großteil des Plasmas wird durch ein MHD-Modell beschrieben, lediglich die energiereichen Teilchen betrachten wir mit einem aufwendigeren kinetischen Modell (Abbildung 1). Ziel dieser Hybridstrategie sind effiziente Algorithmen, die numerische Experimente auch auf kleinen bis mittelgroßen Rechnern ermöglichen.
Energiereiche Teilchen können Plasmawellen grundsätzlich auf zwei verschiedene Arten beeinflussen: über den Gesamtstrom oder über den Drucktensor des Plasmas. Diese beiden Kopplungseffekte kann man über dynamische Prinzipien wie das Wirkungsprinzip herleiten, was garantiert, dass im neuen Hybridmodell physikalische Größen wie Energie oder Impuls erhalten sind [1]. Diese „gute“ dynamische Struktur lässt sich auch in die Computersimulation übertragen, nämlich unter Verwendung sogenannter geometrischer Methoden der Diskretisierung. Diese Methoden berücksichtigen die geometrische Bedeutung einer physikalischen Größe: so führt ein Kraftfeld beispielsweise zu einem Linienintegral, eine Dichte zu einem Volumenintegral. Es hat sich gezeigt, dass derartige geometrische Verfahren zu sehr stabilen Algorithmen führen, was im Hinblick auf die Welle-Teilchen-Resonanzen von Vorteil ist. So können numerische Artefakte aufgrund akkumulierter kleiner Fehler von vornherein ausgeschlossen werden.
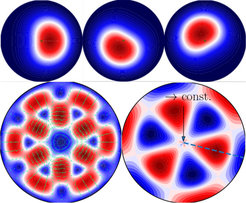
Obwohl die wichtigste Anwendung unseres Verfahrens Fusionsplasmen sind, insbesondere bei ITER, lässt es sich auch auf allgemeine Plasmen zum Beispiel in der Astro- und Geophysik anwenden. So konnten wir zum Beispiel die Wechselwirkung von kalten Plasmawellen mit energiereichen Elektronen im dipolartigen Erdmagnetfeld simulieren und dabei eine nicht-lineare Frequenzmodulierung (chirping) beobachten [2]. Zudem untersuchten wir die Resonanz von verscherten Alfvén-Wellen mit energiereichen Teilchen im Fusionsreaktor vom Typ Tokamak. Hierbei sorgt das besondere Koordinatensystem für eine zusätzliche Schwierigkeit: In der toroidalen (ringförmigen) Geometrie eines Tokamak ist es nämlich sinnvoll, Flusskoordinaten zu verwenden, wobei eine Koordinate den ineinander geschachtelten Flussflächen des magnetischen Feldes in der poloidalen Ebene folgt. Dabei ergibt sich eine Singularität im metrischen Tensor am Mittelpunkt des kleineren Kreises des Torus, das heißt am Ort der magnetischen Achse. Mithilfe neuartiger polarer Spline-Funktionen (Abbildung 2) gelang es uns, die Stetigkeit der numerischen Lösung an der magnetischen Achse sicherzustellen [3]. Dies erwies sich als besonders wichtig in der Kopplung mit energiereichen Teilchen. Außerdem verglichen wir Strom- und Druckkopplung in vereinfachten Geometrien [4]. Die neuen Algorithmen erwiesen sich dabei als sehr verlässlich und zeigten die erwarteten guten Erhaltungseigenschaften auch bei nicht-linearer Welle-Teilchen-Wechselwirkung.
Hybrid-Algorithmen mit Open-Source-Ansatz
Die neuen Hybrid-Algorithmen werden kontinuierlich mit einem Open-Source-Ansatz weiterentwickelt. Hierzu entstand das umfangreiche Python-Software-Paket PSYDAC-STRUPHY (STRUctrure-Preserving-HYbrid codes) (siehe Link in der linken Spalte). Ziel ist es, einer möglichst großen Zahl von Wissenschaftlern einen möglichst einfachen Zugang zur Physik energiereicher Teilchen im Plasma mittels Simulationen zu ermöglichen.













