Forschungsbericht 2020 - Max-Planck-Institut für Evolutionsbiologie
Populationsgenetische Modelle für die Evolution von Antibiotikaresistenz
Die Evolution von Bakterien: Alles andere als langweilig
Auf den ersten Blick scheinen Bakterien recht simple Organismen zu sein: Sie bestehen aus einer einzigen Zelle, und um sich zu vermehren, teilen sie sich. Dabei wird ihr Erbgut kopiert, jede Tochterzelle bekommt eine Kopie, und am Ende liegen – bis auf Mutationen – zwei identische Zellen vor. Man könnte also meinen, dass ihre Evolution eher langweilig ist. So einfach ist es aber nicht.
Plasmide: Extra-DNA in mehreren Kopien
Die essentiellen Gene, die ein Bakterium für Wachstum und Zellteilung braucht, befinden sich auf dem Chromosom. Viele Bakterien besitzen aber noch zusätzliche DNA-Moleküle, sogenannte Plasmide, auf denen sich ebenfalls Gene befinden. Auch Plasmide werden repliziert und an die Tochterzellen vererbt. Sie werden manchmal als Parasiten erachtet: Die Extra-DNA zu kopieren und die Extra-Gene in Proteine zu übersetzen, kostet Energie. Allerdings können die zusätzlichen Gene für das Bakterium auch lebenswichtig sein. Gene für Antibiotikaresistenz finden sich zum Beispiel oft auf Plasmiden. Manche Arten von Plasmiden können an Nachbarzellen weitergegeben werden, mitunter sogar, wenn diese zu einer anderen Bakterienart gehören. Auf diese Weise können Resistenzgene in Bakterienpopulationen eingetragen werden. Die Verbreitung vorhandener Resistenzen ist die prominenteste Art, wie Plasmide zu Antibiotikaresistenz führen. Es ist aber nicht die einzige Art, auf die sie zur Evolution von Bakterien beitragen, denn auch Gene auf Plasmiden können mutieren. Plasmide und damit auch ihre Gene liegen oft nicht nur in einer Kopie vor, sondern in mehreren oder sogar vielen, wobei sie eine charakteristische Kopienzahl pro Zelle aufweisen. Das hat evolutionäre Konsequenzen.
Die evolutionäre Dynamik von Genen auf Plasmiden

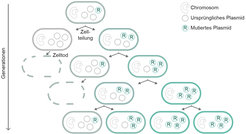
Generell spielt bei genetischer Anpassung Zufall eine große Rolle: Die Entstehung fitter Varianten ist zufällig und ihre Ausbreitung keineswegs garantiert (Abb. 1).
Wie beeinflusst die Anzahl von Plasmiden in einer Zelle die Entstehung von Mutationen und die Wahrscheinlichkeit, dass sie sich tatsächlich in einer Population etablieren? Wenn es viele Kopien gibt, gibt es auch viele Kopiervorgänge, bei denen es zu Mutationen kommen kann. Die Wahrscheinlichkeit von Mutationen auf Plasmiden steigt also mit der Kopienanzahl pro Zelle. Zunächst trägt nur eine der Kopien die Mutation. Durch Kopieren dieser Variante und die zufällige Verteilung der Plasmide auf die Tochterzellen können aber Zellen entstehen, die mehr als eine mutierte Kopie tragen. Dieser Prozess über mehrere Generationen hinweg ist in Abbildung 2 gezeigt. Dass viele Zellteilungen nötig sind, um Zellen mit einer hohen Anzahl mutierter Plasmide zu generieren, steht der Etablierung der Mutation a priori im Weg. Ist eine große Anzahl an Kopien nun also gut oder schlecht?
Die Mathematik von Plasmiden
Um Fragen zur Dynamik von Genvarianten auf Plasmiden zu beantworten, entwickeln wir mathematische Modelle. Dabei nehmen wir an, dass es zwei Varianten eines Plasmids gibt, die ursprüngliche und die mutierte, die zu Resistenz führt. Um die Zufälligkeit der Prozesse zu erfassen, verwenden wir stochastische Modelle, zum Beispiel Verzweigungsprozesse. Letztere sind eine spezielle Art stochastischer Prozesse, die sich durch ihre einfache Struktur sehr gut mathematisch analysieren lässt. Die Untersuchung des Problems mithilfe mathematischer Modelle hat viele Stärken. Durch die klare Formulierung und Analyse ist ein detailliertes Verständnis der Dynamik möglich. Außerdem können schnell viele Szenarien durchgespielt und einzelne Parameter gezielt variiert werden. Im Labor ist das oft nicht möglich oder sehr aufwendig.
Wann sind viele Kopien von Vorteil?
In Modellen können wir den Einfluss der Mutation auf die Fitness der verschiedenen Zellarten beliebig festsetzen. Wir haben uns bisher auf Szenarien konzentriert, in denen keine Zelle fitter ist als diejenigen, in der alle Kopien mutiert sind. Hier muss man aber noch verschiedene Fälle unterscheiden. Zum Beispiel kann es sein, dass bereits Zellen mit einem einzigen mutierten Plasmid resistent sind (dominante Mutation) oder aber dass alle Kopien mutiert sein müssen (rezessive Mutation). In beiden Fällen nimmt die Etablierungswahrscheinlichkeit mit der Anzahl an Kopien pro Zelle ab. In unseren Modellen sieht man, dass die Wahrscheinlichkeit für Resistenzevolution trotzdem zunimmt, wenn die erforderliche Mutation dominant ist. Bei rezessiven Mutationen hingegen sinkt die Wahrscheinlichkeit erfolgreicher Anpassung, je mehr Kopien sich in der Zelle befinden. Wichtig sind auch Fälle, in denen nicht die relative, sondern die absolute Zahl mutierter Plasmide über den Grad der Resistenz entscheidet. In solchen Fällen kann die Etablierungswahrscheinlichkeit mit der Anzahl an Kopien ansteigen.
Aber wie ist nun der Zusammenhang zwischen der Anzahl mutierter Plasmide und der Resistenz einer Zelle? Als ein Beispiel haben wir die Produktion eines Enzyms modelliert, dessen mutierte Variante das Antibiotikum unschädlich macht. Dabei zeigte sich, dass eine derartige Mutation – vorausgesetzt, ihre relative Häufigkeit ist entscheidend – bei niedrigen Antibiotikakonzentrationen einer dominanten Mutation ähnelt, bei hohen jedoch einer rezessiven. Wenn wir dies mit unseren anderen Ergebnissen kombinieren, sehen wir, dass sich diejenige Kopienanzahl, für die Resistenzevolution am wahrscheinlichsten ist, mit der Konzentration ändert.
Mathematik und Biologie
Die Modellierung der Dynamik von Genvarianten auf Plasmiden vereint schöne Mathematik mit der Nähe zum Experiment, und Modellierung und Experiment stehen in engem Wechselspiel. Experimentell arbeitende Forschungsgruppen untersuchen die Anpassung durch neue Genvarianten auf Plasmiden im Labor. Anhand der Beobachtungen können Modellannahmen überprüft und verbessert und Vorhersagen getestet werden. Mathematische Modelle wiederum erlauben eine detailliertere Analyse des Prozesses und können dadurch helfen, empirisch erlangte Ergebnisse zu erklären oder zu untermauern - und neue Experimente anregen.

