Forschungsbericht 2012 - Max-Planck-Institut für Dynamik und Selbstorganisation
Turbulente Muster
Turbulenz breitet sich aus
Will man Kaffee und Milch etwa für einen Latte Macchiato übereinander schichten, so muss der Kaffee sehr behutsam in die aufgeschäumte Milch gegossen werden. Andernfalls bilden sich turbulente Wirbel, die die Flüssigkeiten schnell vermischen. Dasselbe Phänomen lässt sich auch an anderer Stelle beobachten, etwa bei aufsteigendem Rauch (Abb. 1): Ruhig und gleichmäßig bleibt die Strömung nur, wenn sich das Fluid langsam bewegt. Bei höheren Geschwindigkeiten bilden sich zeitabhängige, chaotische Wirbel – die Strömung wird turbulent. Sobald eine Turbulenz einsetzt, entwickelt sie die für chaotische Systeme typische extreme Empfindlichkeit gegenüber Anfangsbedingungen und Störungen. Dies macht es unmöglich, etwa atmosphärische Störungen langfristig vorherzusagen. Auch Wettervorhersagen, die mehrere Tage in die Zukunft schauen, sind unsicher.

Die Entstehung von Turbulenz wird seit mehr als Hundert Jahren in Laborexperimenten untersucht – unter anderem in geometrisch einfachen Situationen wie der druckgetriebenen Strömung durch ein Rohr mit kreisförmigem Querschnitt [1]. Ein anderes typisches Beispiel ist die nach dem französischen Mathematiker Maurice Couette benannte Strömung einer Flüssigkeit zwischen zwei parallelen Platten, die sich mit konstanter Geschwindigkeit gegeneinander bewegen. In diesen Beispielen für sogenannte Scherströmungen reicht eine bestimmte Strömungsgeschwindigkeit oder Reynoldszahl alleine nicht aus, um die Strömung turbulent werden zu lassen. Stattdessen ist zusätzlich eine Störung endlicher Stärke erforderlich, da die laminare Strömung gegenüber infinitesimalem Stören stabil bleibt.

Abb. 2: Turbulenter Spot in einer Kanalströmung zwischen zwei parallelen Glasplatten: Wird die ruhige laminare Strömung kurzzeitig durch einen kleinen Wasserstrahl senkrecht zur Fließrichtung (von links nach rechts) gestört, bildet sich ein turbulenter Bereich. Dieser breitet sich langsam aus.
Wird etwa die laminare Couette-Strömung zwischen zwei Platten an einem Punkt gestört – z. B. durch einen zusätzlichen Strahl oder auch durch einen Kratzer in der ansonsten glatten Wand – so entsteht ein turbulenter „Spot“. Dies ist ein räumlich begrenzter Bereich turbulenter Wirbel, der von laminarer Strömung umgeben ist (Abb. 2). Im Laufe der Zeit wächst dieser Spot und breitet sich wie ein Waldbrand in den laminaren Strömungsbereich hinein aus, bis die gesamte Strömung turbulent geworden ist [2].
Bisher haben Wissenschaftler weder die Dynamik, noch die Ausbreitung der Turbulenz in der Couette-Strömungen vollständig verstanden. Zwar sind die Navier-Stokes-Gleichungen, welche die Strömungen mathematisch beschreiben, genau bekannt und turbulente Spots und ihre Ausbreitung können in Computersimulationen reproduziert werden. Allerdings sind die Lösungen der nichtlinearen partiellen Differentialgleichung nicht einfach zu charakterisieren, sodass nicht im Detail verstanden ist, wie die Gleichungen die beobachteten Phänomene erzeugen. Die physikalischen Mechanismen des Turbulenzübergangs bleiben damit weiter rätselhaft.
Turbulenz und Chaos
Vom chaotischen Verhalten turbulenter Strömungen sind die Menschen seit Jahrhunderten fasziniert. Der Wunsch, turbulente Dynamik zu verstehen, war auch eine der Motivationen, die in der zweiten Hälfte des 20. Jahrhunderts die Entwicklung der Theorie dynamischer Systeme („Chaostheorie“) anregte [3].
Diese mathematischen Untersuchungen haben unter anderem zu zwei grundlegenden Erkenntnissen geführt. Selbst in sehr einfachen Modellsystemen und trotz der genauen Kenntnis der Gesetzmäßigkeiten, nach denen sich ein System entwickelt, machen sensitive Abhängigkeiten von Störungen Vorhersagen über den zukünftigen Zustand des Systems praktisch unmöglich . Gleichzeitig lassen sich die „typischen“ und mittleren Zustände (hier etwa Strömungsmuster) durch spezielle, einfache Lösungen der Systemgleichungen charakterisieren. In einfachen Modellsystemen konnten die Eigenschaften dieser speziellen Lösungen (es handelt sich dabei zum einen um „Fixpunkte“ – also zeitlich unveränderliche Lösungen – oder um „periodische Orbits“, bei denen das System nach einer bestimmten Zeit wieder zu seinem ursprünglichen Zustand zurückkehrt) sowie ihre Bedeutung bei der Entstehung von Chaos genau verstanden und dadurch sogar allgemeinere Mechanismen für die Entstehung von Chaos identifiziert werden.
Obwohl diese Überlegungen auch vom Ziel, Turbulenz zu verstehen, motiviert waren, ließen sich die Konzepte lange nicht von einfachen Modellsystemen auf die deutlich komplexeren, turbulenten Strömungen übertragen. Dies liegt daran, dass die erwähnten speziellen Lösungen sich nicht berechnen ließen.
Weil Strömungen durch nichtlineare partielle Differentialgleichungen, die Richtung und Betrag der lokalen Strömungsgeschwindigkeit an jedem Ort gleichzeitig beschreiben, charakterisiert werden, ist ihre Lösung nur mit leistungsfähigen Computern möglich.
Turbulenz im Computer
Diese Computer stehen seit einiger Zeit zur Verfügung. In den vergangenen Jahren haben Forscher deshalb begonnen, die speziellen Strömungsmuster in einfachen Geometrien zu berechnen sowie ihre Eigenschaften und dynamischen Verbindungen untereinander zu beschreiben [4]. Damit ist die Forschung durch die Kombination moderner Hochleistungsrechner mit mathematischen Modellen, die an einfachen Modellen entwickelt wurden, dem Traum näher gekommen, der die Pioniere der Chaostheorie ursprünglich motiviert hatte: die Entstehung von Turbulenz zu verstehen.
Trotz aller Fortschritte können die bisher bekannten speziellen Lösungen aber nur einen Teil der beobachteten Phänomene beschreiben. Die Lösungen sind räumlich periodisch und konnten unter Ausnutzung ihrer Translationssymmetrie in verhältnismäßig kleinen Gebieten mit periodischen Randbedingungen berechnet werden. Diese Lösungen ähneln damit einer ebenen Welle – sie sind räumlich unendlich ausgedehnt und können damit begrenzte Muster wie sich ausbreitende turbulente Spots nicht beschreiben. Anders als etwa in der Elektrodynamik oder Quantenmechanik, die auf linearen Gleichungen basieren, lassen sich in der nichtlinearen Navier-Stokes-Theorie auch keine lokalisierten Wellenpakete durch Überlagerung vieler ausgedehnter ebener Wellen konstruieren. Die bekannten Lösungen beschreiben deshalb zwar Aspekte der zeitlichen Dynamik (also der lokalen Fluktuationen der turbulenten Strömung), nicht aber die Entwicklung auf großen räumlichen Skalen. Diese spielen jedoch gerade beim Anwachsen eines Spots eine entscheidende Rolle.
Um die volle raum-zeitliche Dynamik des Turbulenzübergangs mit den Methoden beschreiben zu können, die im Rahmen der Chaostheorie entwickelt wurden, sind daher im Raum lokalisierte, spezielle Lösungen notwendig.
Musterbildung
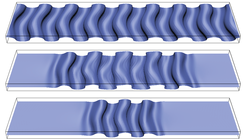
Eine erste Gruppe dieser lokalisierten Lösungen konnte für die Couette-Strömung in der Tat kürzlich konstruiert werden (Abb. 3) [5]. Es handelt sich dabei um eine ganze Familie lokalisierter Versionen der ältesten räumlich ausgedehnten, periodischen Lösung in Couette-Geometrie [6]. Besonders spannend, unerwartet und bisher nicht vollkommen verstanden ist die Tatsache, dass die lokalisieren Lösungen mit ihren ausgedehnten Entsprechungen über einen Mechanismus verbunden sind, den wir aus anderen Gebieten der nichtlinearen Physik kennen – nämlich aus der Theorie der Musterbildung in Nicht-Gleichgewichtssystemen. Dieselben Mechanismen, die mit streifenförmigen Gen-Expressions-Verteilungen in frühen Stadien der Fliegenembryo-Entwicklung und den charakteristischen Mustern vieler Tierfelle in Verbindung gebracht werden, scheinen auch die lokalisierten Lösungen der Navier-Stokes-Gleichung in Couette-Geometrie zu erzeugen.
Dieser unerwartete Zusammenhang zwischen lokalisierten Lösungen der Strömungsgleichungen und klassischen Musterbildungsmechanismen ermöglicht ein systematisches Verständnis der Beziehung zwischen räumlich periodischen Lösungen und ihren im Raum modulierten „Verwandten“. Dies wird es – so die Hoffnung – ermöglichen, nicht nur die zeitliche, sondern die gesamte raumzeitliche Dynamik von Strömungen am Übergang zur Turbulenz zu verstehen.
Mögliche Anwendungen
Die dargestellten neuen Ansätze werden dazu führen, dass Wissenschaftler raumzeitliche Effekte, wie das Wachstum turbulenter Spots, immer besser verstehen. Dies wird zu einem tieferen Verständnis turbulenter Strömungen in genau dem Sinne führen, wie es den Pionieren der Chaosforschung vorschwebte.
Gleichzeitig erwarten wir praktische Anwendungen im Bereich der Turbulenzkontrolle: Nicht nur in der Couette-Strömung, sondern auch in praktisch relevanteren Situationen wie der Grenzschichtströmung über einer Tragfläche entsteht Turbulenz meist aus einem lokalen Herd und breitet sich rasch aus. Will man diese Ausbreitung effektiv verhindern, etwa weil die zusätzliche turbulente Reibung die Energiedissipation erhöht, so gelingt dies am besten, wenn man die genauen Mechanismen der Ausbreitung versteht und so beeinflussen kann [7].
Insgesamt hat uns die Anwendung von Konzepten der Chaos- und Musterbildungstheorie in Kombination mit modernen Computersimulationen weit gebracht: Sie hat unser Verständnis von Turbulenz und ihrer Entstehung deutlich vertieft. Wie weit diese neuen Ansätze tragen werden, wird sich in den nächsten Jahren herausstellen – auf jeden Fall bleibt die Turbulenzforschung spannend.


