Forschungsbericht 2009 - Max-Planck-Institut für Physik komplexer Systeme
Neuartige Ordnungsphänomene in frustrierten Quantenmagneten
Neue Quantenzustände der Materie (Dr. Andreas Läuchli)
MPI für Physik komplexer Systeme, Dresden
Magnetische Ordnung ist eines der faszinierendsten Phänomene. Magnetische Momente – zum Beispiel mit einem magnetischen Dipolmoment ausgestattete Ionen im Festkörper – sind bei hohen Temperaturen im Allgemeinen ungeordnet, da die thermische Bewegung sie in alle Richtungen fluktuieren lässt. Bei tieferen Temperaturen spielt die Wechselwirkung zwischen den Momenten eine zunehmend wichtigere Rolle. In gewissen Systemen ist die Wechselwirkung so stark, dass ein Phasenübergang in eine geordnete Phase auftritt, in der die magnetischen Momente sich kollektiv entlang einer spontan gewählten Richtung ausrichten. Eisen ist ein bekanntes Material, in dem solche magnetische Ordnung unterhalb der Curie-Temperatur von 1040 Kelvin einsetzt. Dies ist ein konkretes Beispiel für spontane Symmetriebrechung, ein Konzept, das in vielen Bereichen der Physik von großer Bedeutung ist.
Bis vor zwanzig Jahren lag ein Hauptaugenmerk in dem Gebiet auf dem vertieften Verständnis der Natur der geschilderten Phasenübergänge, abhängig von der Gitterstruktur und Dimensionalität des Materials und der Art der Wechselwirkung. Dabei wurde verstanden, dass die Phasenübergänge in Universalitätsklassen fallen, das heißt, dass die Art des Übergangs nicht von allen mikroskopischen Details abhängt, sondern nur von qualitativen Faktoren, wie zum Beispiel der Natur der gebrochenen Symmetrie oder der Raumdimension. Die diskutierten Phasen blieben aber meist eine paramagnetische Phase bei hohen Temperaturen sowie eine magnetisch geordnete Phase bei tiefen Temperaturen.

In der letzten Zeit sind neue Gesichtspunkte ins Zentrum des Interesses gerückt. Zum einen sind die magnetischen Momente in der Natur quantenmechanische Objekte, und die Größe der magnetischen Momente von z.B. Kupfer Cu2+ beträgt S=1/2, was dem kleinstmöglichen (von Null verschiedenen) Wert entspricht. In dem Fall könnte man erwarten, dass die Quantenfluktuationen eine sehr wichtige Rolle spielen und zum Beispiel dazu führen, dass die magnetische Ordnung durch die Fluktuationen zerstört wird. Zum anderen hat das Konzept der Frustration enorm an Bedeutung gewonnen [1]. Frustration bezeichnet die Unmöglichkeit eines Systems, alle individuellen Beiträge zur Energie simultan zu minimieren. Betrachten wir zum Beispiel ein System von diskreten Spins (+1,-1) auf einem Gitter, in dem sich benachbarte Spins entgegengesetzt (antiferromagnetisch) ausrichten möchten (siehe Abb. 1). Im Falle eines Quadratgitters gibt es genau zwei Arten dies zu erreichen (zwei Schachbrettermuster von +1 und -1 Spins), und die Energie ist minimal, d.h. das System ist nicht frustriert. Im Falle des Dreiecksgitters gelingt das hingegen nicht. Nachdem man zwei Spins auf einem Dreieck antiparallel ausgerichtet hat, so kann der dritte Spin nicht mehr gleichzeitig antiparallel zu beiden anderen Spins angeordnet werden. In diesem Falle spricht man von Frustration. Die Wichtigkeit dieses Konzepts rührt daher, dass auf dem Dreiecksgitter eine exponentielle Anzahl an Zuständen existiert, die das (frustrierte) Energieminimum erreichen. In dieser Situation werden die thermischen oder quantenmechanischen Fluktuationen extrem wichtig und können zu neuartigen Phasen führen, die mit der ursprünglichen magnetischen Ordnung wenig gemeinsam haben. Im Folgenden werden zwei spezifische Phänomene genauer beschrieben, die im Wechselspiel von Quantenfluktuationen und Frustration auftreten können und in unserer Arbeitsgruppe untersucht werden.
Singlett-Kristalle: Spontane Strukturbildung durch Frustration

Eine der Möglichkeiten für ein frustriertes magnetisches System mit S=1/2 Spins ist, die Rotationsinvarianz gar nicht erst zu brechen (Quantenparamagnet), die räumliche Symmetrie hingegen schon. Dies wird erreicht, indem das Gitter spontan mit Singlett-Einheiten dekoriert wird. Ein Singlett ist hier ein kollektiver Quantenzustand einer geraden Zahl von S=1/2 Spins, bei dem der Gesamtspin verschwindet. Der Mechanismus hinter diesem Phänomen ist die modulierte Verteilung der Frustration, um letztendlich eine niedrigere quantenmechanische Energie zu erzielen. Abhängig von der zugrundeliegenden Gitterstruktur werden sehr verschiedene Strukturen beobachtet. In der Abbildung 2 links ist ein Kagome-Gitter zusammen mit einem häufig diskutierten Singlett-Kristall dargestellt [2]. Die spontan gebildete Struktur umfasst zwölf Einheitszellen des Ausgangsgitters mit insgesamt 36 Spins. Das ist eine der größten Einheitszellen, die bis jetzt in zweidimensionalen frustrierten Magneten gefunden wurde. In der Abbildung 2 rechts werden Korrelationsfunktionen in einem durch zusätzliche Kopplungen frustrierten Quadratgitter gezeigt [3]. Hier sind die spontan gebildeten Einheiten Singlett-Quadrate mit vier Spins, die sich in einem kollektiven S=0 Zustand befinden. Diese neuen Singlett-Einheiten bilden dann eine modulierte Superstruktur auf dem Quadratgitter.
Spin-nematische Phasen: partielle Wiederherstellung der spontan gebrochenen Spin-Rotationssymmetrie
In einer magnetisch geordneten Phase zeigt jeder Spin in eine gewisse Richtung im Spinraum. Dadurch ist die Rotationssymmetrie im Spinraum spontan gebrochen. Es stellt sich nun die Frage, ob Zustände oder Phasen existieren, in denen die Spins keine definite Richtung aufweisen und dennoch die Rotationssymmetrie im Spinraum brechen. Im Folgenden werden solche Zustände allgemein spin-nematisch genannt [4, 5].

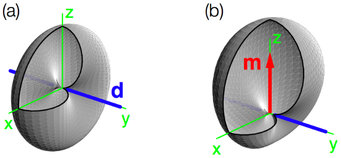
Als Konzept existieren solche Zustände schon über vierzig Jahre. Insbesondere für S=1 Spins ist es einfach, die gewünschten Zustände zu konstruieren. In der Abbildung 3 (a) wird das Fluktuationsellipsoid für eine Sy=0 Wellenfunktion gezeigt. In der y-Richtung sind die Fluktuationen unterdrückt, wohingegen die Fluktuationen in die x- und z-Richtungen endlich sind. Zudem hat dieser Zustand kein Dipolmoment. Man findet auch Beispiele, in denen der Spin ein partielles Dipolmoment in eine Richtung hat und ein Quadrupolmoment in einer transversalen Ebene aufweist, wie in Abbildung 3 (b) dargestellt.
Eine der großen Herausforderungen ist es, mikroskopische Modelle zu finden und zu lösen, die einerseits die gewünschten spin-nematischen Phasen aufweisen und andererseits auch experimentell relevant sind. Kürzlich haben wir eine ganze Reihe von spin-nematischen Phasen in einer vergleichsweise einfachen frustrierten ferromagnetischen Spinkette gefunden [6]. Das ist insofern spannend, als es mehrere Materialien gibt, die sich gut durch solch ein Modell beschreiben lassen, und man somit optimistisch sein kann, dass der erste experimentelle Nachweis von spin-nematischen Phasen in Reichweite liegt.