Forschungsbericht 2020 - Max-Planck-Institut für Chemische Physik fester Stoffe
Der Quanten-Hall-Effekt in der dritten Dimension
Von Klitzing’s Beobachtung des quantisierten Hall-Widerstandes impliziert, dass ein Magnetfeld äußerst effektiv Elektronen durch ein 2D-Metall pumpen kann. Tatsächlich ist es nach den Gesetzen der Quantenphysik unmöglich, in irgendeiner anderen Form effektiver Elektronen durch ein Metall zu treiben. Die unglaubliche Präzision von bis auf ein Millionstel genau, mit der der quantisierte Hall-Widerstand h/e² in 2D-Metallen gemessen werden kann, ist heute Grundlage eines neuen internationalen Einheitensystems, das nur auf Naturkonstanten basiert. Starke Wechselwirkung zwischen Elektronen in Quanten-Hall-Systemen haben zudem zu einer Vielzahl neuer Phänomene und Theorien geführt, wobei der fraktionale QHE das prominenteste Beispiel ist. Außerdem hat der QHE zu einer Neueinteilung von Materialien geführt, der sogenannten topologischen Klassifizierung. Warum ist der Hall-Widerstand in 2D-Metallen so universell quantisiert?
Das Geheimnis des QHEs liegt darin, dass er ein wirklich makroskopisches Quantenphänomen ist, denn das gesamte 2D-Metall verhält sich wie ein einziges Quant. Damit wird auch klar, warum der QHE nur bei tiefen Temperaturen auftritt: Um einen makroskopischen Quantenzustand zu bilden, müssen alle Atome und Elektronen in einem Metall zusammen schwingen. Mit zunehmender Temperatur wächst die chaotische Bewegung der Atome und Elektronen, was ihrer gemeinsamen Schwingung entgegenwirkt. Nur, wenn die Temperatur tief genug ist, kann sich ein makroskopischer Quantenzustand ausbilden. Im Magnetfeld öffnet sich dann über das gesamte 2D-Metall hinweg eine Lücke im Energiespektrum der Elektronen, sodass das Material dann nur noch von eindimensionalen elektrischen Strompfaden durchzogen ist. Durch diese Strompfade können die Elektronen ohne abgelenkt oder gebremst zu werden vom Magnetfeld bewegt werden – wie auf Schienen.
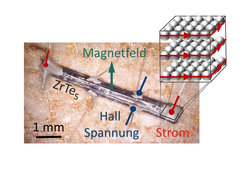
Nun sind 2D-Metalle eher selten in der Natur anzutreffen. Um den QHE beispielsweise für technische Anwendungen nutzbar zu machen, wäre es sehr hilfreich, diesen auch in dreidimensionalen (3D) Metallen zu beobachten. In gewöhnlichen 3D-Metallen ist der QHE allerdings verhindert, da sich in der dritten Dimension entlang des Magnetfeldes keine Energielücke bilden kann. Dadurch werden die 1DStrompfade zu 2DFlächen, auf denen die Elektronen beliebig von ihrer Bahn abgelenkt werden können. Damit wird die Quantisierung des Hall-Widerstandes zerstört. Vor kurzem konnten wir allerdings zeigen, dass in den 3D-Metallen ZrTe5 (Abbildung 1) [2] und HfTe5 [3], eine 3D-Version des QHE auftreten kann. Dieses Phänomen ist auf die ungewöhnlich wenigen Elektronen in ZrTe5 und HfTe5 zurückzuführen, die sich in starken Magnetfeldern in aufeinandergestapelten 2D-Lagen anordnen. Jede dieser Lagen bildet dann ein 2D-Metall mit einem quantisierten Hall-Widerstand.
Damit sich die Elektronen in 2D-Lagen anordnen können, dürfen sich in dem 3D-Metall nur Elektronen befinden, die – im Wellenbild – nur eine bestimmte Wellenlänge lF besitzen. Ohne Magnetfeld sind in einem Metall Elektronen mit vielen unterschiedlichen Wellenlängen vorhanden. Das Magnetfeld verändert die Wellenlängen der Elektronen und sortiert mit ansteigender Magnetfeldstärke immer mehr von ihnen aus, bis nur noch Elektronen einer Wellenlänge übrig sind. Je mehr Elektronen in einem Metall sind, desto größer ist die Vielfalt an Wellenlängen im Metall und desto größer ist das Magnetfeld, das benötig wird, um alle Elektronen in eine einzige Wellenlänge zu überführen.
In normalen 3D-Metallen wie Kupfer, in denen vergleichsweise viele Elektronen existieren, würde dieses Magnetfeld in der Größenordnung von 10.000 T liegen. Das ist etwa 200 Millionen Mal größer als das Erdmagnetfeld in Europa. Selbst das größte jemals auf der Erde erzeugte Magnetfeld mit rund 300 T wäre viel zu schwach. Metalle wie ZrTe5 und HfTe5 sind nun besonders interessant, weil in ihnen nur ungefähr ein Hundertmillionstel der Elektronen von gewöhnlichen Metallen existieren und damit moderate Magnetfelder von etwa 2 T ausreichen, um alle Elektronen in eine Wellenlänge zu überführen. Hinzu kommt ein weiterer Vorteil: Wenn die Elektronen ihre eine Wellenlänge eingenommen haben, ändern sie diese auch bei verändertem Magnetfeld nicht mehr.
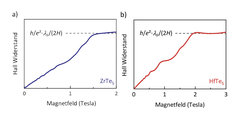
Wie in Abbildung 2a und b gezeigt, beobachteten wir, dass sich im Hall-Widerstand in millimetergroßen Proben von ZrTe5 und HfTe5 ein quantisiertes Plateau bereits bei Magnetfeldern unter 2 T entwickelt. Da in der Messung der 3D-Metalle alle 2D-Lagen und damit deren QHE mitgemessen werden, ist der Hall-Widerstand (durch h/e² geteilt) durch die Anzahl der Lagen gegeben. Die Anzahl der gemessenen Lagen ergibt sich dann daraus, wie viele Elektronen der entsprechenden Größe in die Höhe H der Probe passen: H/(lF/2). In den von uns gemessenen Proben, sind es bis zu einigen zehntausend Lagen. Damit ergibt sich der gesamte Hall-Widerstand des 3D-Metalls zu: RH = h/e²·lF/(2H). In drei Dimensionen hängt der QHE damit nicht nur von Naturkonstanten, sondern auch von dem Probenparameter lF/(2H) ab. In HfTe5 konnten wir zusätzlich auch deutliche Signaturen von Elektronen-Wechselwirkungen beobachten, einschließlich Signaturen des „fraktionalen“ QHE[3].
Es gibt jedoch noch viele offene Fragen. Wenn wir ein Metall mit noch weniger Elektronen als in ZrTe5 und HfTe5 entwerfen könnten, kann dann der QHE auch bei Raumtemperatur oder in Magneten sogar ohne angelegtes Magnetfeld auftreten? Vierzig Jahre nach der Entdeckung, ist der Quanten-Hall-Effekt immer noch so spannend wie am ersten Tag.
Literaturhinweise
Nature Review Physics 2, 397–401 (2020)
Nature Communications, 11, 5926 (2020)

