Multi-scale modelling
Complex materials, ranging from DNA molecules to steel hulls of oil tankers, are affected by processes that span wide ranges of time and space. Critical phenomena can be realistically described by linking computational models of materials at different scales. Successful multi-scale modelling of materials and processes is now predictive and not just descriptive.
Materials surround us—from raw materials such as metal ores in the earth, protein biomaterials in our bodies to functional materials that power electronic devices. Science and engineering demands the utmost of materials, and increasingly their properties are being tested quickly and efficiently using computer modelling1.
Modelling materials-related processes is not simple, as the underlying phenomena span an enormous range of lengths and timescales2,3. For example, although metal corrosion is initiated by electron movements that occur within trillionths of a second, it takes minutes for the first surface layers to form rust and it can take years or centuries for the destructive effects to become significant. The levels of information in computational materials science are generally classified into four regimes. First, at the quantum scale: theoretical calculations and practical experiments describe how electrons behave in atoms, exposing the nature of chemical bonding from which material properties derive; such detailed computations are limited to relatively small groups of several hundred atoms, which are now detailing the behaviour of electrons at the attosecond3,4,11. Second, at the atomistic level: molecular-dynamic calculations simulate movements of millions of atoms and molecules according to known electromagnetic principles; movement can be simulated only for brief periods (billionths of a second). Third, at the mesoscopic scale, computations replace thousands of atoms with an average property, such as mass density, charge or temperature, allowing physical simulations to proceed for longer (from nanoseconds to microseconds). Fourth, at the macroscopic scale: millions of particles are treated as a continuous distribution, and physical properties are solved using classical thermodynamic and kinetic equations. This allows researchers to simulate processes, such as flow through a pipeline or the efficiency of a turbine, in real time.
Connecting these levels is vital for developing multi-scale models that describe and even predict essential materials behaviour5,6. This paper provides three examples of progress towards this goal through developing quantitative design strategies, discovering important natural mechanisms, and using quantum mechanics to predict products and processes.
Unfolding protein secrets
Proteins comprise amino-acid chains that fold into unique shapes within cells. This folding process is central to a protein’s biological function — for example, Alzheimer’s disease is characterized by misfolded amyloid-protein, which agglomerates into plaques. Establishing accurate models of protein structures could lead to breakthroughs in therapeutic treatments.

The intricate interactions that govern protein folding are understood on the quantum scale; however, the timescales — from microseconds to years in vivo — and the millions of atoms constituting protein environments have limited predictive power at this scale. New concepts, algorithms and computer codes have allowed small but relevant quantum simulations, using 100–1,000 atoms, to deliver predictive insights into important biological mechanisms.
For example, consider the behaviour of 15-alanine polypeptide (Fig. 1). Experimentally, this short protein chain forms a helical shape that is thermally stable up to 475°C, but previous computational methods could not account for this behaviour; simulations showed the helix unravelling at high temperatures.
By developing quantum-based simulations that include van der Waals interactions, multi-scale models yielded correct protein structures7,8. Although challenges remain — such as incorporating solvent effects and extending simulation times — these findings demonstrate that simple protein structure, folding and unfolding problems are solvable through computations.
Predicting better implants
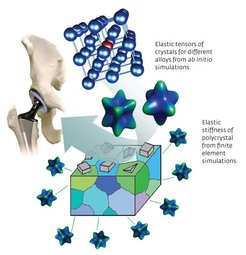
Biomedical implants are increasingly important for ageing populations, but current implants suffer from the stress-shielding effect (Fig. 2). Replacing parts of the skeleton with stiff metal implants shields living bone cells from their accustomed mechanical loads, diminishing bone density, mineralization and strength. Elastically softer materials are thus needed.
In implants such as artificial hip joints, titanium alloys are widely used because of their strength and low toxicity. Titanium implants can be made softer by solidifying them into a crystal structure called the beta phase. However, beta-phase titanium alloys are difficult to make because of their reduced stability.
Instead of an experimental search filled with trial and error, it is possible to use theory-guided design of biomedical materials to screen systematically a series of titanium-niobium alloys for beta-phase stability using quantum-mechanics based computations, and then to use the thermodynamic quantities derived from these calculations as the basis for macroscopic modelling of elastic behaviour.9,10
This approach predicted the design of alloys with roughly half the stiffness of current implants — promising to reduce pain for the millions of patients who receive hip transplants each year. It also opens opportunities for theory-guided design of future biomedical products.
Opening up soft materials
Soft materials form organized systems at scales beyond those of molecules, within products ranging from plastics in yoghurt cups, to foods such as mayonnaise and to biological molecules including DNA. They differ from ‘hard matter’ (such as steel or gold) by lower energy density: the bonds are 100–1,000 times weaker than those in metallic crystals5,6.
Thermal effects influence the organization of soft materials. Hence, models cannot use quantum calculations alone; thermodynamic calculations must also be included.
Modelling soft materials starts with an atomic description, and then derives a broader model for simulations over a longer period. This approach can rapidly switch between levels of resolution, and can be run in reverse to study melting behaviour. Various soft-material problems, such as polymer stability or liquid-crystal switching, can be solved this way.
Future and Perspectives
Imagine moving from a study of individual alloy atoms to simulating the material in an automotive test crash or using the results of biomolecular simulations to describe the workings of blood vessels. Multi-scale modelling could make such visions reality, but challenges remain. Unified theories of matter, which can bridge computational scales in a physically consistent manner, must be developed. Experimental observations are needed to verify model predictions at all levels. Successful multi-scale modelling must be capable of handling the complexity of real-life situations to avoid generating incorrect predictions.
A multiscale model, based on coupled ab initio and continuum simulations, has helped to unravel the molecular and mesoscopic structure and properties of chitin-based natural polymers. These materials form the exoskeleton of arthropods, including insects, spiders and decapods. The model can be used to design advanced synthetic polymers. The project was realized cooperatively by the Max Planck Society, the Bulgarian Academy of Sciences and the Massachusetts Institute of Technology (Nikolov. S. et al. Adv. Mater.22, 519–526, 2010 ).













