Meaningful relationships - mathematical insights into the geometry of complex networks
Networks are complex systems characterized by plenty of connections and interactions between their different actors. The first examples of networks emerged with the first social systems of mankind. In an increasingly interconnected world, investigating our modern society’s complex systems, which are subjected to a constant development and a permanent change, has become one of the great challenges of science.
The underlying structure of networks can be described using a graph, a mathematical object consisting of a number of nodes and edges, which allow implementing connections of different form and strength. To get further insight into the structure of network models, mathematicians have employed classical geometric concepts, like that of curvature, the quantity that measures the extent to which a given surface or space fails to be flat. The concept of curvature is central in mathematics and it permeates different sciences.
Starting from Gauss's work on surfaces, many brilliant minds have occupied themselves with it. The Ricci curvature, a generalization of Gauss's curvature developed by Gregorio Ricci Curbastro around the turn of the 20th century, has been a driving force in the advancement of science and a source of spectacular mathematical results. To begin with, the Ricci curvature was an essential ingredient in Einstein's formulation of General Relativity: it is through the Ricci curvature tensor that “spacetime tells matter how to move, and matter tells spacetime how to curve”*, as described by Einstein's field equations. Hamilton's Ricci flow, a by-product of the Ricci curvature, was used in the proof of the Geometrisation conjecture by Gregori Perelman, for which he was offered the Fields medal in 2006, the highest recognition in mathematics. The Ricci curvature is also central in the work of the 2010 fields medalist Cédric Villani on optimal transport.
The usefulness and profoundness of this concept are further demonstrated by recent applications to network sciences. In order to treat discrete objects like graphs, mathematicians have developed several alternative and somehow simplified versions of the Ricci curvature, each highlighting and emphasizing different aspects of the underlying network. This freedom of choice has lent urgency to a rigorous study on how the different curvatures actually compare when put to test on specific examples like road networks, biological networks, and collaboration networks.
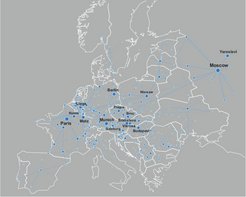
Euro road network where nodes are cities and edges are roads connecting different European cities. The picture shows a portion of the Euro road network limited to the cities with Forman-Ricci curvature ≤ −2 and edges connecting them. Cities with highly negative Forman-Ricci curvature (< −7) are labeled in the figure. Size of nodes and width of edges are proportional to the absolute value of the corresponding Forman-Ricci curvature.
This work constitutes a major first step in this direction, providing not only an empirical comparison of the behavior of the most used discrete versions of the Ricci curvature, namely the Ollivier–Ricci and the Forman–Ricci curvature, but also an affirmative clear-cut answer. After analyzing several different networks and data sets, coming from various fields including the social sciences and biology, the researchers in this interdisciplinary team were able to deduce that the two notions, despite being different in spirit, yield very similar results. Interestingly, the comparison works especially well on real existing networks, like the European road network depicted in the figure. This opens an avenue for the analysis of large networks.
*John Archibald Wheeler in “Geons, Black Holes, and Quantum Foam: A life in Physics (2000)
This paper is a collaborative project of mathematicians in cooperation with computer scientists and biologists. It is in particular supported by the Max Planck Partner Group in Mathematical Biology in IMSc, Chennai, India.












