Forschungsbericht 2015 - Max-Planck-Institut für Sonnensystemforschung
Rotation und Aktivität sonnenähnlicher Sterne
Die Suche nach einer Erklärung der Sternaktivität
Rotation ist eine der wesentlichen Größen, die einen Stern charakterisieren. Ein Stern entsteht, wenn ein Teil seiner ursprünglichen Molekülwolke beginnt, unter dem Eigengewicht zu kollabieren. Diese Wolke rotiert zunächst sehr langsam, doch während sie zusammenfällt, nimmt ihre Rotationsgeschwindigkeit enorm zu.
Das Zusammenspiel von Rotation und Magnetfeldern innerhalb eines Sterns lässt sich durch Dynamomodelle theoretisch beschreiben ([1]) und ist für die Sternaktivität, also Phänomene wie Sternflecken, verantwortlich. Das Verständnis der Physik solcher Systeme ist jedoch unvollständig. Die Beobachtung der Rotation von unterschiedlich alten Sternen mit verschiedenen Massen und Magnetfeldkonfigurationen wird helfen, die Mechanismen, welche die Sternaktivität verursachen, besser zu verstehen.
Messungen der oberflächennahen Rotation mit Hilfe von Sternflecken
Die Kepler-Mission der NASA lieferte eine Vielzahl an Daten, um die Rotation von Sternen zu studieren. Das Ziel dieser Mission war es, die Häufigkeit von erdähnlichen Planeten bei anderen Sternen zu bestimmen. Dazu beobachtet Kepler kontinuierlich über mehrere Jahre hinweg bestimmte Regionen am Himmel. So lassen sich Helligkeitsvariationen von mehr als 200 000 Sternen messen. Diese Messungen, auch Lichtkurven genannt, werden für die Erforschung von Exoplaneten benutzt, liefern aber zusätzlich auch viele Informationen über die Sterne selbst.
In diesen Lichtkurven ist auch das Signal von Sternflecken enthalten. Rotiert der Stern, passieren die dunklen Sternflecken regelmäßig seine sichtbare Seite und reduzieren dabei seine Gesamthelligkeit. Wandern die Flecken wieder auf die Rückseite des Sterns, nimmt seine Gesamthelligkeit wieder ihren normalen Wert an. Über mehrere Tage oder Monate hinweg beobachtet, lässt sich aus diesen Helligkeitsschwankungen die Rotation der äußeren Schichten des Sterns messen.
Mit dieser Methode wurde ein Katalog der Sternrotationsraten von mit Kepler beobachteten Sternen erstellt [2]. Anhand einer eigens hierfür entwickelten, automatisierten Rechenroutine ließen sich die Rotationsraten von mehr als 12 000 Sternen bestimmen– mehr als zehn Mal so viele wie bis dahin verfügbar. Anschließend wurden die Ergebnisse speziell für sonnenähnliche Sterne mit vorherigen Studien verglichen, die auf Spektroskopie beruhen. (siehe Abb. 1). Mit dieser Methode lässt sich die Rotation von tausenden von Sternen zuverlässig ermitteln. Nur anhand einer so umfassenden Stichprobe lässt sich verstehen, wie einzelne Sterne im Vergleich zur Gesamtpopulation rotieren.
Auf dieser Grundlage wurden fünf Sterne gezielt ausgewählt, da sie neben Sternflecken auch stellare Oszillationen (interne seismische Wellen) mit einem hohen Signal-zu-Rausch-Verhältnis aufweisen[3].
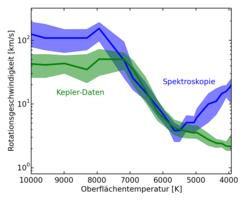
Abb. 1: Mit Hilfe von Sternflecken aus Kepler-Daten ließ sich die mittlere Rotationsgeschwindigkeit von etwa 12000 Sternen als Funktion der Oberflächentemperatur der Sterne (grün) ermitteln. Die blaue Kurve zeigt unabhängige Messungen der Rotation (für andere Sterne) mittels Spektroskopie. Sonnenähnliche Sterne haben eine Temperatur von etwa 5500 bis 6500 Kelvin. Hier liefern Sternflecken eine sehr zuverlässige Messung der Rotation.
Messungen der Rotationsrate im Inneren mittels Asteroseismologie
Sonnenähnliche Sterne oszillieren mit einer Periode von etwa fünf bis zehn Minuten. Diese Schwingungen sind im Wesentlichen Schallwellen, die von der Rotation des Sterns beeinflusst werden. Breiten sich die Wellen in der Drehrichtung des Sterns oder genau entgegengesetzt aus, werden sie Doppler-verschoben. Anhand von Messungen dieser Dopplerverschiebung (hier auch „Rotationsaufspaltung“ genannt) lässt sich die Rotationsrate des Sterns in seinem Inneren bestimmen. Da verschiedene Wellenmoden unterschiedlich tief in den Stern vordringen, weisen Differenzen in der Stärke der Dopplerverschiebung auf eine tiefenabhängige Rotationsrate hin.
Abb. 2 zeigt für den Stern KIC006116048 einen kleinen Ausschnitt des Leistungsspektrums (links) sowie die Abhängigkeit der Dopplerverschiebung von der Frequenz der Wellenmode (rechts). Es gibt keine klar erkennbaren Anzeichen für eine Abhängigkeit der Rotationsrate von der Tiefe.
Für die Sonne ließ sich mit dieser Methode der Asteroseismologie ein detailliertes Bild der solaren Rotationsrate in Abhängigkeit der Tiefe gewinnen. Für andere Sterne gelang diese Bestimmung der sogenannten differenziellen Rotation jedoch bisher nicht mit vergleichbarer Güte. Grund dafür ist die enorme Entfernung: Im Gegensatz zur gleißend hellen Sonnenscheibe, in der sich selbst kleine Strukturen beobachten lassen, erscheinen andere Sterne lediglich als lichtschwache Punkte. Auch wenn wir die mittlere Rotationsgeschwindigkeit der Sterne recht leicht messen können, lassen sich genauere Rotationsprofile nur äußerst schwer bestimmen.
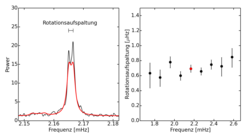
Abb. 2: Links: Stärke der Oszillationen als Funktion der Frequenz (Leistungsspektrum) in einem kleinen Bereich um die Resonanzfrequenz des Sterns KIC006116048 herum (schwarz). Der Abstand zwischen den beiden Peaks entspricht der Rotationsfrequenz des Sterns. Er lässt sich bestimmen, indem man ein Modell an die Daten fittet (rot). Rechts: Da unterschiedliche Wellen in unterschiedliche Tiefen vordringen, können etwaige Differenzen in den Peak-Abständen durch eine tiefenabhängige Rotationsrate des Sterns hervorgerufen werden.
Eingrenzen der differentiellen Rotation
Allein anhand von Asteroseismologie Informationen über die differentielle Rotation eines Sterns zu gewinnen, ist also schwierig (siehe Abb. 2). Wenn man jedoch zusätzliche Informationen über die Rotation aus anderen Quellen erhalten kann (z. B. aus Sternflecken), ist es möglich, Modelle, die weniger gut passen, auszuschließen. So lassen sich Leitplanken für die Theorien aufstellen, aus denen die Modelle abgeleitet werden. Zurzeit existiert eine Vielzahl von unterschiedlichen Modellen, um magnetische Dynamos in Sternen sowie die Aufrechterhaltung der differentiellen Rotation in der Sonne zu erklären. Mit solchen kombinierten Messungen aus Asteroseismologie und Sternflecken ließen sich diese Modelle nun klar eingrenzen, und einige können vielleicht sogar komplett ausgeschlossen werden.
Die Sonnenrotation ist charakterisiert durch einen starr rotierenden inneren Bereich, der etwa 70 Prozent des Sonnenradius ausmacht, und eine davon unabhängig rotierende Hülle darüber. Viele Modelle der magnetischen Aktivität in sonnenähnlichen Sternen gehen von einem ähnlichen Rotationsprofil aus. Allerdings ist unklar, ob dies gerechtfertigt ist.
Wird ein solch einfaches Rotationsprofil für sonnenähnliche Sterne angenommen, besteht das Ziel darin, die Differenz der Rotationsraten zwischen Innerem und der Hülle zu messen. Die asteroseismischen Messungen der Rotationsraten in beiden Zonen sind jedoch entartet, d. h. es lässt sich nicht einfach sagen, aus welchem Teil des Sterns ein beobachteter Effekt in den asteroseismischen Daten herrührt.
Dieses Problem lässt sich lösen, indem die Rotationsraten der Sternflecken als zusätzliche Randbedingung für die Rotation der Hülle herangezogen werden. Dies erlaubt es, einen Großteil der möglichen asteroseismischen Lösungen auszuschließen. Abb. 3 zeigt die Ergebnisse dieser Vorgehensweise exemplarisch für einen Stern.
Für die Sonne liefert dieses simple Modell eine Differenz von 0,1 Mikrohertz zwischen den Rotationsraten der Kern- und der äußeren Zone. Die verfügbaren Daten für die fünf analysierten Sterne zeigen, dass eine Differenz größer als 0,5 Mikrohertz sehr unwahrscheinlich ist, sofern man von dem Zwei-Zonen-Modell ausgeht. Auch lässt sich aufgrund des Rauschniveaus in den Messungen nicht ausschließen, dass das Sterninnere und die Hülle in manchen Fällen sogar gleich schnell rotieren. Nichtsdestotrotz eliminieren diese Messungen einen großen Teil der Modelle, welche auf Differenzen von mehr als 0,5 Mikrohertz angewiesen sind. Vorher war der Wert dieser Größe völlig unbekannt.
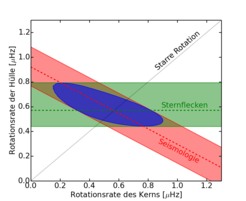
Abb. 3: In Rot sind die möglichen asteroseismischen Lösungen für die Rotationsraten von Innerem und Hülle des Sterns KIC004914923 aus der untersuchten Messreihe dargestellt. Es gibt viele Lösungen, die denselben Effekt in den Messdaten erzeugen. Durch die Einbeziehung der Sternflecken kann jedoch die Rotationsrate der Hülle eingegrenzt und somit die Menge der Lösungen deutlich reduziert werden (blau). Die gestrichelte schwarze Linie macht deutlich, dass eine gleich schnelle Rotation von Sterninnerem und Hülle nicht ausgeschlossen werden kann.
Die Zukunft: Die PLATO-Mission
Bei der Messung der Rotation von sonnenähnlichen Sternen stößt man zurzeit an die Grenze dessen, was mit Kepler-Daten möglich ist. Kepler hat etwa einhundert helle sonnenähnliche Sterne beobachtet.
Die PLATO-Mission [5] der europäischen Weltraumagentur, die 2024 gestartet werden soll, wird hochpräzise Messungen der stellaren Oszillationen von etwa einhunderttausend hellen sonnenähnlichen Sternen liefern. Die Beobachtung dieser umfassenden Stichprobe wird unser physikalisches Verständnis, was ihre Aktivität und Rotation betrifft, vertiefen und die Sonne in einen größeren Rahmen einbetten. So wird man beispielsweise durch die Anwendung der Asteroseismologie für eine Stichprobe von tausend Sternen mit ähnlichem Alter sowie ähnlichen Massen und Radien ein gemitteltes Rotationsprofil messen können, dessen Präzision etwa dreißigmal höher ist als für einen einzelnen Stern. Damit wird man bestimmen können, wie die Rotation im Inneren über die verschiedenen Typen von Sternen variiert.
Das wichtigste Ziel von PLATO und der große Vorteil im Vergleich zu Kepler ist allerdings, dass die asteroseismisch durchgeführten genauen Messungen der fundamentalen stellaren Parameter verwendet werden können, um präzise Rückschlüsse auf Radien, Massen und Alter von Planeten zu ziehen, die mit Hilfe der Transitmethode um diese Sterne entdeckt wurden. Das Ziel ist es, einige erdähnliche Planeten zu entdecken, die sonnenähnliche Sterne umkreisen. Die Atmosphäre dieser Planeten könnte dann von der Erde aus weiter mit hochpräziser Spektroskopie untersucht werden.
Literaturhinweise
Saas-Fee Advanced Courses 39, Springer, 2013
Astronomy & Astrophysics, 557, L10 (2013)
Experimental Astronomy, 38, 249-330 (2014)


