Die Geometrie der Krebszelle
Bösartige und gesunde Zellen weisen charakteristische fraktale Muster auf, anhand derer sie sich unterscheiden lassen
Ein neuer Ansatz lässt auf eine Methode hoffen, mit der sich Krebszellen künftig schneller und zuverlässiger unterscheiden lassen könnten. Wissenschaftler des Max-Planck-Instituts für Intelligente Systeme in Stuttgart und der Universität Heidelberg haben festgestellt, dass sich Zellen sehr genau mithilfe der fraktalen Geometrie charakterisieren lassen. Mit dieser Theorie werden Objekte beschrieben, deren Struktur im Kleinen ihrer Gestalt im Großen ähnelt. Krebszellen können ihr Wachstum und damit ihre Gestalt verglichen mit gesunden Zellen schlechter regulieren. Die spezielle fraktale Geometrie einer Zelle wird damit zu einem Marker für den Zelltyp. Daher lässt sich der Erkrankungsgrad einer Zelle mit dieser Mathematik, kombiniert mit einer geschickten Bilderkennung, analysieren. Die Forscher untersuchten, in welcher statistischen Verteilung welche Strukturdetails auf der Oberfläche von unterschiedlichen Tumorzellen auftreten. Auf diese Weise konnten sie Krebszellen genauer erkennen, als das mit der bisher gängigen immunhistologischen Methode möglich ist, und zwischen Zellen verschiedener Tumore unterscheiden.

Den Begriff Fraktal gibt es noch nicht einmal seit 40 Jahren, fraktale Strukturen aber schon seit Urzeiten. Denn die Blätter eines Farns, der Romanesco-Blumenkohl und Meeresküsten sind so aufgebaut, dass sich ihre geometrischen und topographischen Eigenschaften wiederholen, wenn man sie stärker vergrößert. Auch die Auswüchse und Ausstülpungen auf den Oberflächen von Zellen zeigen solche selbstähnlichen Muster. Wie Forscher um Joachim Spatz, Direktor am Max-Planck-Institut für Intelligente Systeme in Stuttgart und Professor an der Universität Heidelberg, nun festgestellt haben, lassen sich Tumorzellen und gesunde Zellen anhand ihrer fraktalen Geometrie unterscheiden.
Die Wissenschaftler vergrößerten die Ränder von Zellen der Bauchspeicheldrüse und analysierten deren Unregelmäßigkeiten. Indem sie diese mathematisch erfassten, bestimmten sie die fraktale Dimension des Zellrandes, die ein Maß für die statistische Verteilung der Unregelmäßigkeiten ist. Krebszellen weisen einen höheren Fraktalisierungsgrad auf als gesunde Zelle, da sich beim unkontrollierten Tumorwachstum sehr unregelmäßige Ausbuchtungen verschiedener Größe auf der Zelloberfläche bilden. Die Forscher erkannten an der fraktalen Dimension aber nicht nur, ob eine Tumorzelle vorlag, sondern bestimmten mit 97prozentiger Sicherheit auch, um welchen von zwei unterschiedlich bösartigen Bauchspeicheldrüsentumoren es sich handelt. „Auf diese Weise lassen sich Krebszellen sehr viel genauer und schneller unterscheiden als mit der bisher gängigen Methode“, sagt Joachim Spatz.
Krebszellen zu identifizieren, ist bisher unsicher und zeitaufwendig
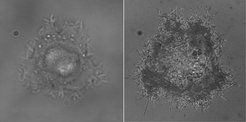
Bisher werden Krebszellen und ihr Entstehungsort im Körper identifiziert, indem eine per Biopsie entnommene Zellprobe mit bestimmten Antikörpern und Biomarkern eingefärbt wird. Die Färbemethode hat jedoch Nachteile: Sie erfordert zahlreiche Einzelschritte mit kostspieligen Antikörpern und ist daher zeitaufwendig und teuer. Außerdem können die derzeit gebräuchlichen Farbstoffe feinste Unterschiede von Zellen nicht immer sichtbar machen. Daher lässt sich ein Krebs mit dieser Methode nur in 85 Prozent der Proben korrekt diagnostizieren.
Mithilfe der fraktalen Geometrie erkennt das Team von Joachim Spatz Krebszellen nicht nur zuverlässiger, sondern das geht auf diese Weise auch deutlich schneller. Denn die Zellen lassen sich unter einem Mikroskop untersuchen, ohne dafür besonders präpariert werden zu müssen. Um die Details der Zellränder erfassen zu können, verwendet das Team von Joachim Spatz ein Reflexionskontrastmikroskop. Statt die Probe wie ein herkömmliches Lichtmikroskop von unten zu durchleuchten, misst das Mikroskop der Stuttgarter Forscher die Reflexion des Lichtstrahls an der Zelloberfläche. Diese ist unterschiedlich, je nachdem, ob das Licht direkt auf eine Zelle oder zuerst auf wässriges Zellkulturmedium und dann auf eine Zelle trifft. Anhand des reflektierten Lichtes lassen sich selbst winzige Strukturen am Zellrand untersuchen.
„Die fraktale Geometrie der Zelloberflächen zu analysieren, birgt ein sehr großes Potenzial für die klinische Diagnostik“, sagt Spatz. Nun erforschen die Wissenschaftler, wie sich ihre Methode in der Praxis anwenden lässt. Dazu untersuchen sie unterschiedliche bösartige Zelllinien und primäre Zellen, also solche Zellen, die aus menschlichen Organen gewonnen werden und die im Gegensatz zu Tumorzelllinien nur über eine bestimmte Zeitspanne kultiviert werden können. „Der nächste Schritt für uns werden konkrete Kooperationen mit Kliniken sein, um die Methode direkt an relevanten Gewebeproben zu testen“, erklärt Joachim Spatz.
NG/KH /PH