Forschungsbericht 2011 - Max-Planck-Institut zur Erforschung von Gemeinschaftsgütern
Die Logik der richterlichen Überzeugungsbildung
Von der inneren Überzeugung zur vernünftigen Überzeugung
Richter sind an die Gesetze gebunden. In der Feststellung der ihrer Urteile zugrunde liegenden Tatsachen sind sie aber laut Gesetz frei. Diese Freiheit in der Beweiswürdigung ist eine historische Errungenschaft, denn bis Ende des 18. Jahrhunderts waren Richter an gesetzliche Beweisregeln gebunden. So mussten sie etwa eine Tatsache als gegeben erachten, wenn sie von zwei „klassischen“ Zeugen – Personen, die nicht wegen ihrer Beziehung zu den Parteien oder wegen Vorstrafen eine verminderte Glaubwürdigkeit besaßen – bezeugt wurde. Solche Beweisregeln konnten zu Ergebnissen führen, die von den meisten Menschen als im Widerspruch zur Wirklichkeit stehend empfunden wurden. Dies wurde aber als für die Voraussehbarkeit des Prozesserfolges zu bezahlender Preis in Kauf genommen.
Während der Französischen Revolution wurden in Frankreich, dem englischen Vorbild folgend, für Strafsachen Geschworenengerichte eingeführt. Aus Misstrauen gegenüber dem staatlichen Richter wollte man Bürger über Mitbürger richten lassen. Da von juristischen Laien nicht erwartet werden konnte, dass sie die umfangreichen gesetzlichen Beweisregeln kennen, mussten diese Regeln im Geschworenenprozess weichen. Die Geschworenen sollten verurteilen, wenn sie zur inneren Überzeugung (conviction intime) gekommen waren, dass der Angeklagte die ihm vorgeworfene Tat begangen hatte.
In Deutschland stieß die französische Lehre von der „inneren Überzeugung“ anfänglich auf Widerstand. Alleine den bloßen „Totaleindruck“, das „dunkle Gefühl“, darüber entscheiden zu lassen, ob eine Tatsache als wahr zu erachten sei, schien der Willkür Tür und Tor zu öffnen. Dort, wo man Geschworenengerichte einführte, wurde die Freiheit in der Beweiswürdigung als notwendige Begleiterscheinung akzeptiert, aber wo juristisch ausgebildete Richter zuständig blieben – namentlich in Zivilsachen – wurde die freie Beweiswürdigung überwiegend abgelehnt.
Allmählich setzte sich jedoch die Erkenntnis durch, dass auch die freie Beweiswürdigung nicht willkürlich sein muss. Betont wurde, dass Richter sich ihre Überzeugung vernünftig bilden müssen, dass die Überzeugungsbildung ein rationaler Denkvorgang, kein nicht zu vermittelndes Empfinden, sei. Die richterliche Überzeugung ist demnach keine rein innere Überzeugung, sondern eine vernünftige Überzeugung, eine conviction raisonée. Seinen Ausdruck fand dieses Verständnis in der auch heute noch verwendeten Formulierung, dass Richter an die „Denkgesetze und Erfahrungssätze“ gebunden sind. Ein Verstoß gegen die Denkgesetze ist ein Verstoß gegen das Gesetz und führt zur Aufhebung des Urteils.
Welche Überzeugungen kann man vernünftigerweise gleichzeitig haben?
Als Inhalt dieser Denkgesetze wurde lange Zeit die klassische (aristotelische) Logik gesehen. In den 1930er-Jahren wiesen jedoch zwei Mathematiker, der Engländer Frank P. Ramsey und der Italiener Bruno de Finetti, unabhängig voneinander darauf hin, dass es eine Logik der Überzeugungsbildung gebe und dass diese Logik den Gesetzen der Wahrscheinlichkeitstheorie gehorche (der sogenannten „subjektiven Wahrscheinlichkeitstheorie“) [1, 2]. Nach dieser Auffassung lässt sich der Überzeugungsgrad dafür, dass eine Tatsachenbehauptung wahr ist, in einer Wettquote ausdrücken. Wer eine Wettquote von 1:4 dafür, dass es morgen regnet, als fair akzeptiert – das heißt, wem es egal ist, welche Seite der Wette er bei dieser Wettquote einnimmt – der hat einen Überzeugungsgrad von 20 Prozent dafür, dass es morgen regnet (bei einer Wettquote von 1:4 erhält man bei einem Einsatz von 1 Euro eine Auszahlung von 5 Euro, wenn man die Wette gewinnt).
Die Theorie macht keine Aussagen darüber, welchen Überzeugungsgrad jemand anfänglich dafür hat, dass eine Tatsachenbehauptung wahr ist. Sie lässt aber die Behauptung zu, dass es irrational ist, gewisse Überzeugungen gleichzeitig zu halten: So muss, nach der Theorie, diejenige, die zu 20 Prozent überzeugt ist, dass es morgen regnet, zu 80 Prozent überzeugt sein, dass es morgen nicht regnet. Und wer zu 20 Prozent glaubt, dass es morgen regnet, kann nicht gleichzeitig zu 15 Prozent überzeugt sein, dass es morgen Vormittag regnet und zu 10 Prozent, dass es morgen Nachmittag regnet. Solche gleichzeitig gehaltenen Teilüberzeugungen werden als inkohärent bezeichnet.
Die Theorie schreibt weiter vor, wie man seine Überzeugungen im Lichte neuer Information ändern muss, ohne dass sie inkohärent im vorgenannten Sinne werden (nach der sogenannten „Bayes-Regel“). Man kann darin ein Modell richterlicher Überzeugungsbildung sehen, denn Richter passen ihre Überzeugung, dass eine Tatsachenbehauptung wahr ist, im Lichte der in den Prozess eingeführten Beweismittel an [3, 4]. In der juristischen Literatur wurde, beginnend in den frühen 1970er-Jahren in den USA und seit den 1980er-Jahren in einem geringeren Ausmaß auch in Deutschland, ein erbitterter Streit darüber geführt, ob diese Theorie als Modell richterlicher Überzeugungsbildung taugt. Es wurde infrage gestellt, ob man eine Überzeugungsbildung, die ihr gehorcht, tatsächlich als „rational“ bezeichnen kann.
Grafische Darstellung von Teilüberzeugungen
Ein berechtigter Einwand gegen die Theorie ist, dass es einem Menschen faktisch unmöglich ist, kohärente Teilüberzeugungen im Sinne der subjektiven Wahrscheinlichkeitstheorie zu haben. Außerhalb des Bereichs einfachster Lehrbuchbeispiele übersteigt dies schlicht die Kapazität des menschlichen Gehirns. Ein weiterer Einwand ist, dass dort, wo es an empirisch erhobenen statistischen Daten fehlt, die „Berechnung“ eines Überzeugungsgrades nur zu einer Scheingenauigkeit führe, die darüber hinwegtäusche, dass die ihr zugrunde liegenden Annahmen keine Basis in der Wirklichkeit zu haben brauchen.
Tatsächlich ist es so, dass diese Theorie zur Erfassung komplexer Sachverhalte mit zahlreichen Beweismitteln wenig geeignet war. Ende der 1980er-Jahre wurde jedoch in der Forschung zur künstlichen Intelligenz ein Durchbruch erzielt, indem grafische Modelle der Überzeugung, so genannte Belief Nets oder Bayesian Networks, die Modellierung auch komplexer Zusammenhänge erlaubten [5]. Technisch gesehen machen sich Bayes-Netze die bedingten Unabhängigkeiten zwischen Variablen zunutze, um die gemeinsame Wahrscheinlichkeitsverteilung kompakt darzustellen. Sie bestehen aus einem Graphen bestehend aus knotengerichteten Verbindungen zwischen den Knoten und mit den Knoten verbundenen bedingten Wahrscheinlichkeitstafeln. Für den Anwender ist wesentlich, dass man die Pfade zwischen den Knoten in einem solchen Netzwerk als kausale Einflüsse verstehen kann, und es fällt Menschen erheblich leichter, in kausalen Zusammenhängen als in statistischen Zusammenhängen zu denken.
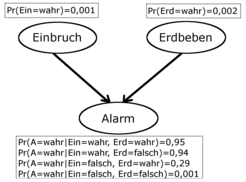
Abbildung 1 zeigt ein einfaches Beispiel: Ein Alarm kann entweder durch einen Einbruch oder ein Erdbeben ausgelöst werden. Wenn ich erfahre, dass der Alarm ausgelöst wurde, steigt meine Überzeugung dafür, dass eingebrochen wurde, ebenso wie meine Überzeugung, dass ein Erdbeben stattgefunden hat. Die subjektive Wahrscheinlichkeitstheorie sagt mir, wie sehr sich die Überzeugung ändern muss, ohne dass meine gleichzeitig gehaltenen Überzeugungen inkohärent im vorher dargestellten Sinn werden. Im konkreten Beispiel führt die Anwendung der Bayes-Regel dazu, dass die Überzeugung dafür, dass eingebrochen wurde, bei ausgelöstem Alarm von 0,1 auf 37 Prozent steigt. Das ist erheblich mehr als die anfängliche Überzeugung für einen Einbruch, aber weit weniger als die Wahrscheinlichkeit, dass der Alarm ausgelöst wird, wenn eingebrochen wird (die mehr als 94 Prozent beträgt).
Wenn ich weiter erfahre, dass kein Erdbeben stattgefunden hat, muss meine Überzeugung dafür, dass eingebrochen wurde, gemäß der subjektiven Wahrscheinlichkeitstheorie auf rund 48 Prozent steigen. Weil es (mindestens) zwei mögliche Ursachen für den Alarm gibt und eine ausgeschlossen werden kann, ist es wahrscheinlicher, dass die andere Ursache vorliegt. Diesen Effekt nennt man explaining away (einer möglichen Ursache), und seine Modellierung durch Bayes-Netze ist einer der Vorteile der Verwendung solcher Netze. Informationen propagieren sich im Netz, und das Modell erlaubt Aussagen darüber, wie sich die Teilüberzeugungen unter den getroffenen Annahmen ändern müssten, wenn die Überzeugungsbildung rational wäre.
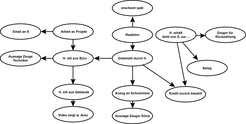
Bayes-Netze erlauben die (relativ) einfache Erfassung komplexer Zusammenhänge. Abbildung 2 zeigt ein Bayes-Netz eines Sachverhalts, der in der psychologischen Forschung zur Überzeugungsbildung im juristischen Kontext eingesetzt wird [6]. Ein Richter muss sich eine Überzeugung dazu bilden, ob ein Diebstahl durch den Angeklagten H. begangen wurde. Das Netz erlaubt ihm zu testen, welchen Einfluss verschiedene Annahmen auf diese Überzeugung gemäß der subjektiven Wahrscheinlichkeitstheorie haben müssen. Es erlaubt also die Aussage, welche Teilüberzeugungen er haben muss, damit er zu einem bestimmten Überzeugungsgrad dafür, dass H. einen Diebstahl begangen hat, kommen kann. Das Netz erzwingt die Kohärenz im Sinne der Theorie, in dem es keine widersprüchlichen Überzeugungen zulässt.
Erfährt man den Zustand einer bestimmten Variablen, so kann diese Information im Netz erfasst werden. Weiß man beispielsweise, dass ein Überwachungsvideo festhielt, dass ein Auto des Typs wie H. eines fährt kurz nach dem Tatzeitpunkt vom Tatort wegfuhr, so setzt man den Zustand der entsprechenden Variablen „Video zeigt w.[eißes] Auto“ auf „wahr“. Die Information wird im Netz über die Knoten „H. eilt aus dem Gebäude“ und „H. eilt aus dem Büro“ unter anderem an den Knoten „Diebstahl durch H.“ weitergegeben. Somit kann man dem Netz entnehmen, wie sich die Überzeugung dafür, dass H. den Diebstahl begangen hat, rational betrachtet ändern müsste, wenn man erfährt, dass eine entsprechende Videoaufnahme vorhanden ist.
Auch das Netz kann dem Richter nicht sagen, welche Teilüberzeugungen mit der Wirklichkeit übereinstimmen. Indem es aber aufzeigt, welche Teilüberzeugungen ein Richter haben muss, um beispielsweise zu einer Überzeugung von mehr als 90 Prozent dafür, dass H. ein Dieb ist, zu kommen, erlaubt es zumindest eine Diskussion über die Plausibilität dieser Annahmen. Es erlaubt auch zu testen, welchen Einfluss unterschiedliche Annahmen auf die Überzeugungsbildung haben. Damit ermöglicht es insbesondere auch eine informierte Entscheidung darüber, in welchen Fällen es sich lohnt, weitere Ressourcen für die empirische Begründung der Annahmen zu verwenden.
Es wird vorausgesetzt, dass eine vernünftige Überzeugungsbildung, wie sie dem Richter vorgeschrieben ist, den Grundsätzen der Wahrscheinlichkeitstheorie gehorchen muss. Mit Bayes-Netzen steht erstmals ein Hilfsmittel zur Verfügung, das die zahlreichen Teilüberzeugungen, die ein Richter haben muss, damit er zu einem bestimmten Überzeugungsgrad für die Wahrheit einer rechtserheblichen Tatsachenbehauptung kommen kann, transparent und damit intersubjektiv diskutierbar macht. Damit wird ein rationaler Diskurs über die Beweiswürdigung bei zahlreichen widersprüchlichen Beweismitteln ermöglicht. Allerdings kann die Modellierung alleine niemals garantieren, dass die richterliche Überzeugung der Wirklichkeit entspricht. Ähnlich wie die deduktive Logik erlaubt sie keine Aussagen zur Wahrheit der Prämissen – hier: Plausibilität der Teilüberzeugungen –, sondern nur dazu, welche Schlüsse bei gegebenen Prämissen (Teilüberzeugungen) zulässig sind.

