Forschungsbericht 2009 - Max-Planck-Institut für Plasmaphysik, Teilinstitut Greifswald
Transport-Simulationen für Wendelstein 7-X
Stellaratortheorie (Prof. Dr. Per Helander)
MPI für Plasmaphysik, Teilinstitut Greifswald
Das Magnetfeld von Wendelstein 7-X wird im Wesentlichen durch dreidimensional geformte supraleitende Spulen erzeugt; im Gegensatz zum Tokamak wird kein Plasmastrom für den Plasmaeinschluss benötigt. Die Dreidimensionalität erlaubte es bei der Konzeption der Anlage, die magnetischen Konfigurationen hinsichtlich unterschiedlicher Plasmaeigenschaften zu optimieren.
Optimierungskriterien für Wendelstein 7-X
Die wichtigsten Optimierungskriterien des Stellarators Wendelstein 7-X sind erstens hohe Gleichgewichts- und Stabilitätsgrenzen und zweitens guter neoklassischer Einschluss des Plasmas. Der neoklassische Transport der Plasmateilchen aus dem Einschlussbereich hinaus beruht auf den radialen Driften der geladenen Teilchen im inhomogenen Magnetfeld. Drittens wurde Wendelstein 7-X auf niedrigen Bootstrap-Strom hin optimiert, ein im ringförmigen Plasma verlaufender Nettostrom, der durch den Plasmadruck getrieben wird. Viertens wurde guter Einschluss schneller Teilchen angestrebt. In einem späteren Kraftwerk dieser Bauart wären also auch die energiereichen Helium-Teilchen, die bei der Fusion entstehen, genügend gut eingeschlossen.
Der gewünschte kleine Netto-Ringstrom ist die Voraussetzung für einen Inseldivertor am Plasmarand – eine Komponente, die für die Reinhaltung des Plasmas sorgt: Der Plasmarand eines Stellarators spaltet sich – der Symmetrie des Magnetfeldes folgend – in einzelne Ausläufer auf. Diese „Inseln“ liegen aneinandergereiht wie die Perlen einer Kette um den Querschnitt des Plasmas und lenken Energie und Teilchen auf begrenzte Bereiche der Gefäßwand. Werden diese Flächen durch Prallplatten geschützt, dann können die hier auftreffenden Teilchen zusammen mit den Verunreinigungen aus dem Plasma entfernt werden.
Der Bootstrap-Strom beeinflusst die Rotationstransformation, d. h. die Verdrillung der Feldlinien, also der Anzahl der poloidalen Umläufe einer Feldlinie pro toroidalem Umlauf in der ringförmigen Konfiguration. Schließen sich die Feldlinien nach wenigen toroidalen Umläufen in sich selbst, dann bilden sich magnetische Inseln, deren radiale Position durch den Plasmastrom verändert wird. Da Wendelstein 7-X ein recht flaches Profil der Rotationstransformation besitzt, muss die Rotationstransformation am Plasmarand und somit der Plasmastrom relativ genau kontrolliert werden, um ausreichend große Inseln am Plasmarand zu erhalten.
Der Plasmadruck verändert die magnetische Konfiguration: Einerseits werden die Flussflächen bei steigendem Druck nach außen verschoben – die sogenannten Shafranov-Verschiebung, andererseits senkt der poloidale diamagnetische Strom (der durch die radialen Plasmadruckgradienten getrieben wird) das Magnetfeld ab. Die charakteristische Größe hierbei ist β, das Verhältnis von Plasmadruck zum magnetischen Druck. Der gewünschte, möglichst hohe Plasmaenergieinhalt entspricht einem hohen, über das Plasmavolumen gemitteltem Wert <β>.
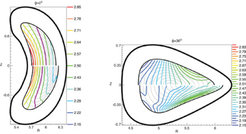
Abbildung 1 zeigt den Einfluss des Plasmadrucks für die Standard-Konfiguration von Wendelstein 7-X in den beiden Symmetrieebenen für <β> = 0 (oben) und 4 Prozent (unten). Bei hohem <β>-Wert verschiebt sich die Resonanzfeldstärke für die Mikrowellenheizung (Elektronen-Zyklotron-Resonanz-Heizung, ECRH) bezüglich der magnetischen Flussflächen stark nach innen, die Effekte der Shafranov-Verschiebung und der Absenkung der Magnetfeldstärke durch den diamagnetischen Strom addieren sich. Die externe Magnetfeldstärke muss daher erhöht werden, um die ECRH-Absorption innerhalb der zentralen Flussflächen auch bei höherem Plasmadruck sicherzustellen.
Bei noch höheren <β>-Werten entsteht ein Minimum der Magnetfeldstärke bei den zentralen Flussflächen, das die ECRH-Absorption in diesem zentralen Bereich verhindert. In der Dreiecksebene (rechts) fällt die Feldstärke von außen nach innen, die Variation ist deutlich kleiner. In der Bohnenebene sind alle Konfigurationen vertikal stark elongiert; dies führt zu einer Verkleinerung der mittleren toroidalen Krümmung des Magnetfeldes und ist sehr wichtig für die Optimierung des neoklassischen Einschlusses.
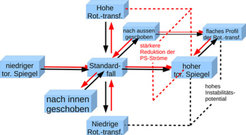
Eine grobe Übersicht über die magnetischen Konfigurationen in Wendelstein 7-X, die durch unterschiedliche Ströme im Spulensystem erzeugt werden können, gibt Abbildung 2. Die unerwünschte Shafranov-Verschiebung wird – durch eine weitere Unterdrückung der Pfirsch-Schlüter-Ströme – stärker reduziert bei höherer Rotationstransformation, bei einer Verschiebung des Plasmas nach innen und bei höherem toroidalem Spiegel (grob das Verhältnis der Magnetfeldstärke in der Bohnen- und der Dreiecksebene des Plasmas). Die Stabilitätseigenschaften dagegen verschlechtern sich bei niedrigerer Rotationstransformation, bei einer Verschiebung nach außen und bei höherem toroidalem Spiegel. Den stärksten Einfluss auf den neoklassischen Einschluss hat der toroidale Spiegelterm. Der Bootstrap-Strom sinkt mit wachsendem Spiegel und wechselt sogar das Vorzeichen bei sehr hohen Werten: Die Hochspiegel-Konfiguration ist nahezu ohne Bootstrap-Strom. Die Standard-Konfiguration zeigt den besten neoklassischen Einschluss, der sich mit steigendem Plasmadruck sogar noch weiter verbessert. Optimaler Einschluss und minimaler Bootstrap-Strom lassen sich nicht in einer einzigen Konfiguration erreichen. Der Einschluss schneller Ionen wird in der Hochspiegel-Konfiguration bei hohem <β> wesentlich verbessert. (Im Modellplasma von Wendelstein 7-X entsprechen schnelle Protonen mit 60 Kiloelektronenvolt den Helium-Teilchen in einem Fusionskraftwerk.)
Transport-Simulationen
Rechnerisch lassen sich die Eigenschaften der unterschiedlichen magnetischen Konfigurationen von Wendelstein 7-X prognostizieren. Neoklassische Transport-Simulationen erlauben eine optimistische Vorhersage der Temperaturprofile und Bootstrap-Ströme, die in den verschiedenen Konfigurationen von Wendelstein 7-X zu erwarten sind. In diesen Simulationen werden die jeweiligen neoklassischen Transportkoeffizienten als Funktion von Dichte, Temperatur und radialem elektrischen Feld benutzt. Nur am Plasmarand bei niedrigen Temperaturen, wo der neoklassische Transport sehr klein wird, wird ein einfaches anomales Transportmodell addiert, das den turbulenten Transport simulieren soll. Die Simulationen sind in dem Sinne optimistisch, dass im inneren Plasmabereich mögliche turbulente Transportbeiträge vernachlässigt werden. Bisher werden die Dichteprofile fest vorgegeben, da sich die wesentlichen Recycling-Quellen, zum Beispiel von den Wänden eindringendes Neutralgas, am Plasmarand befinden, wo die turbulenten Transportbeiträge dominieren. Die Plasmaheizung durch ECRH ebenso wie durch Neutralteilchenheizung (NBI) für positive und negative Ionen (mit 60 bzw. etwa 250 Kiloelektronenvolt) wird selbstkonsistent mit der zeitlichen Entwicklung der Profile behandelt. Für Stellaratoren muss ferner das radiale elektrische Feld Er aus der Ambipolaritätsbedingung berechnet werden. Letztere besagt, dass der flussflächengemittelte radiale Strom verschwinden muss. Die neoklassischen Transportkoeffizienten hängen, besonders bei kleinen Stoßfrequenzen, sehr stark von Er ab.
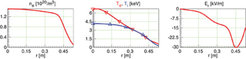
Eine Simulation einer High-performance-Entladung für die Standard-Konfiguration mit <β> von ungefähr 4 Prozent zeigt Abbildung 3. Die ECRH mit 8 Megawatt eingestrahlter Leistung wird unter diesen Bedingungen sehr gut absorbiert. Das relativ stark zentrierte Heizprofil der Elektronen führt zu hohen zentralen Elektronentemperaturen. Die Temperaturen der Elektronen sind wesentlich höher als die der Ionen, da die Ionen nur über Stöße mit den Elektronen geheizt werden. Das ambipolare elektrische Feld Er ist unter diesen Bedingungen negativ, d. h. der neoklassische radiale Ionentransport wird stark reduziert, um die Ambipolaritätsbedingung zu erfüllen. Diese Simulation ergibt einen Plasmaenergie-Inhalt von 4,8 Megajoule entsprechend einer Energieeinschlusszeit τE von 0,6 Sekunden und einen gemittelten Druck <β> von ungefähr 4,2 Prozent. Neoklassische Transport-Simulationen dieser Art zeigen, dass in Wendelstein 7-X recht hohe <β>-Werte bei voller Magnetfeldstärke von 2,5 Tesla erreicht werden könnten. Im Gegensatz zu Hoch-β-Experimenten in anderen Stellaratoren, die bei wesentlich niederen Magnetfeldstärken ausgeführt werden mussten, erlaubt die starke neoklassische Transportoptimierung im Wendelstein 7-X die Kombination von Hoch-β- und High-performance-Szenarien, falls der turbulente Transportbeitrag im Plasmainneren nicht dominiert. Der Bootstrap-Strom von 91 Kiloampere in diesem Beispiel (Abb. 3) ist allerdings viel zu hoch sowohl für erfolgreichen Divertor-Betrieb (in der Konfiguration ohne Berücksichtigung des Stromes) als auch für eine Kompensation durch EC-Stromtrieb (ECCD). Entweder muss also die Rotationstransformation in der Vakuum-Konfiguration entsprechend abgesenkt werden oder aber ein solcher Entladungstyp muss in der Hoch-Spiegel-Konfiguration ausgeführt werden, in der der Bootstrap-Strom minimiert, der neoklassische Einschluss aber etwas schlechter ist.

Eine Übersicht der unterschiedlichen Transport-Simulationen für Wendelstein 7-X zeigt Abbildung 4 bezüglich der Energieeinschlusszeit τE im Vergleich zum ISS04-Skalierungsgesetz, das aus sehr unterschiedlichen Entladungen in verschiedenen Stellaratoren gewonnen wurde. Die sehr hohe Transportoptimierung im Wendelstein 7-X bezüglich der neoklassischen Transportkoeffizienten wird durch die stark nichtlineare Temperaturabhängigkeit reduziert: τE verdoppelt sich etwa im Vergleich zur Skalierung, folgt aber ihrer Tendenz. Die Verschlechterung bei großen τE ergibt sich in NBI-Simulationen mit positiven Ionen bei hohen Dichten, in denen ein großer Teil der Heizleistung dicht am Plasmarand deponiert wird. Diese Verschlechterung des globalen Einschlusses tritt in entsprechenden NBI-Simulationen mit negativen Ionen mit zentraler Deposition nicht auf. Äquivalente Simulationen ohne neoklassische Transportoptimierung, d. h. für einen Wendelstein 7-X ähnlichen klassischen Stellarator, liegen dicht bei der ISS04-Skalierung.
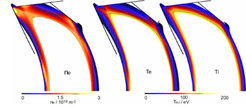
Der Transport in der Randschicht in optimierten Divertorszenarien wird mit einem anderen Code berechnet, der zurzeit noch nicht mit dem neoklassischen Transport im Plasmainneren gekoppelt ist. Dieser Randschicht-Code basiert auf einer Flüssigkeitsbeschreibung des Transports: Der Transport parallel zum Magnetfeld ist klassisch. Anomale Koeffizienten, die turbulenten Transport simulieren, werden nur für den Transport senkrecht zum Magnetfeld angenommen. Sowohl der Teilchen-, der (parallele) Moment- als auch der Energietransport werden selbstkonsistent berechnet. Teilchenquellen in der Randschicht werden im Wesentlichen durch die Flüsse der Recycling-Neutralen mit Ionisation und Rekombination beschrieben. Abbildung 5 zeigt ein Beispiel der Transport-Simulation in der Randschicht für die Standard-Konfiguration. Die Elektronendichte ne ist dicht am Pumpspalt des Divertors (links oben) durch das stark lokalisierte Recycling recht hoch und erlaubt damit gute Pumpeffizienz. Im Bereich des hohen Recyclings sind allerdings auch die Energieflüsse auf die Divertorplatten erhöht; dies reflektiert sich in den höheren Temperaturen.
Die Simulationen des Randschichttransports zeigen eine hohe Empfindlichkeit bezüglich der magnetischen Konfiguration im Divertorbereich, zum Beispiel der Inselposition, was eine recht genaue Kontrolle zum Beispiel des Plasmastroms erforderlich macht. Da sich der Plasmastrom ohne Kompensation durch Stromtrieb – per ECRH und NBI – nur sehr langsam auf seinen stationären Wert einstellt (bis zu 100 Sekunden), kommt der Minimierung des Bootstrap-Stroms eine hohe Bedeutung zu. Die Hoch-Spiegel-Konfigurationen in Wendelstein 7-X mit minimalem Bootstrap-Strom sind daher die natürlichen Konfigurationen für einen optimalen quasi-stationären Betrieb des Inseldivertors, auch wenn der neoklassische Einschluss etwas verschlechtert ist. Andererseits können maximierte High-performance-Entladungen recht kurz sein (einige τE) und ohne optimalen Betrieb des Inseldivertors auskommen.




