Forschungsbericht 2005 - Max-Planck-Institut für Plasmaphysik, Teilinstitut Greifswald
Instabilitäten und Turbulenz im Plasma von Wendelstein 7-X
Stellaratortheorie (Prof. Dr. Per Helander)
MPI für Plasmaphysik, Teilinstitut Greifswald
Die beiden Anlagentypen „Tokamak“ und „Stellarator“ sind derzeit die beiden aussichtsreichsten Kandidaten, um in ringförmigen (torusartigen bzw. toroidalen) Maschinen mit magnetischem Einschluss Kernfusion zu erreichen. Während ein Tokamak rotationssymmetrisch und daher zweidimensional ist, besitzt ein Stellarator nur eingeschränkte diskrete Symmetrien. Er ist deshalb seiner Natur nach dreidimensional, weshalb seine numerische Behandlung einen größeren Rechenaufwand erfordert. Allerdings eröffnet die Dreidimensionalität weitgehende Freiheiten bei der Festlegung des magnetischen Gleichgewichtes, die bei modernen Stellaratoren wie etwa Wendelstein 7-X mittels der so genannten Stellaratoroptimierung ausgenutzt werden. Dabei versucht man durch geeignete numerische Hilfsmittel die Form des Plasmas so zu gestalten, dass vorher festgelegte Kriterien erfüllt werden, die einen guten Einschluss des Plasmas gewährleisten.
Eine wesentliche Größe zur Charakterisierung einer Plasmakonfiguration ist die Rotationstransformation. Diese Kennzahl gibt an, wie oft sich eine verdrillte Feldlinie um den kleinen Plasmaradius herumbewegt (poloidale Richtung), während sie einmal den Torus umkreist (toroidale Richtung). Für die Fusion nötig sind Gleichgewichte, bei denen jede Magnetfeldlinie jeweils eine torusartige Fläche aufspannt, wobei diese so genannten magnetischen Flächen ineinander verschachtelt sind. Der Wert der Rotationstransformation ist auf jeder Fläche verschieden und somit eine Funktion des kleinen Radius.
Zusätzlich zur unterschiedlichen – zwei- bzw. dreidimensionalen – Geometrie unterscheiden sich Tokamak und Stellarator grundsätzlich im radialen Verlauf der Rotationstransformation: Für einen Tokamak nimmt sie zum Plasmarand hin ab. Hier wird die Feldlinienverdrillung des durch äußere Magnetspulen aufgebauten Hauptfeldes durch einen im Zentrum des Plasmas fließenden Plasmastrom erzeugt. In einem Stellarator hingegen wird die Feldlinienverdrillung ausschließlich durch die außerhalb des Plasmas gelegenen Magnetspulen erzeugt, was eine nach außen ansteigende Rotationstransformation bedingt. Definitionsgemäß verschwindet für eine solche Konfiguration in ihrer reinen Form der gesamte toroidale Plasmastrom auf jeder magnetischen Fläche.
Instabilitäten im Plasma
Von Nutzen sind nur solche Konfigurationen, bei denen Plasma und Magnetfeld im Gleichgewicht sind, die also im Idealfall ohne Störung beliebig lange existieren könnten. In einem Gleichgewicht kommt es allerdings immer wieder durch verschiedenste Effekte – zum Beispiel durch kleinste Veränderungen der Dichte oder Temperatur des Plasmas – zu Störungen, deren Entwicklung Gegenstand der Stabilitätstheorie ist. Falls eine kleine Störung von selbst abklingt, ist das Plasma stabil; dies ist die in der Praxis erwünschte Situation. Die globale Variation zum Beispiel der Temperatur, die im Plasma vom Zentrum zum Rand um zwei Größenordnungen abfällt, führt in der Regel zu einer Anfachung einer Störung; das Plasma ist dann instabil.

Eine große und sehr gut untersuchte Klasse von Instabilitäten, die so genannten magnetohydrodynamischen Instabilitäten (MHD-Instabilitäten), besitzen eine großräumige Struktur von der Größenordnung des kleinen Plasmaradius. Treten solche Instabilitäten auf, so führen sie häufig zu einer vollständigen Zerstörung des Plasmagleichgewichtes. Für die theoretische Beschreibung dieser Klasse von Instabilitäten kann das Plasma als eine leitende Flüssigkeit angesehen werden, die sich in einem Magnetfeld bewegt.
Stellaratoren können so optimiert werden, dass verbleibende Instabilitäten und Turbulenz gekennzeichnet sind durch eine kleine Skalenlänge senkrecht zum magnetischen Feld und eine große Skalenlänge in paralleler Richtung. Hier spiegelt sich die starke Anisotropie wieder, die dem System durch das magnetische Feld aufgeprägt wird. Diese so genannten Mikroinstabilitäten wirken auf einer Längenskala, die um ein Vielfaches kleiner ist als der Radius des Plasmas. Ihr Anwachsen führt allerdings nicht zu einer vollständigen Zerstörung des Plasmas, sondern zur Ausbildung einer kleinskaligen turbulenten Bewegung, die Teilchen und Energie aus dem Plasmainneren nach außen transportiert, der so genannte „anomale Transport“. Zur Beschreibung dieser Klasse von Instabilitäten reicht die einfache magnetohydrodynamische Theorie nicht mehr aus: Je nach Bereich – Kern oder Rand mit hoher bzw. niedriger Temperatur und Dichte – muss das Plasma kinetisch (d.h. als aus geladenen Teilchen bestehendes Gas) oder durch zwei elektromagnetisch in Wechselwirkung tretende Flüssigkeiten (Elektronen- und Ionenflüssigkeit) beschrieben werden.
Man hat heute gut verstanden, wodurch magnetohydrodynamische Instabilitäten des Plasmas in Tokamaks und Stellaratoren entstehen und wie sie verhindert werden können. Hingegen scheinen Mikroinstabilitäten sowie die aus ihnen entstehende Turbulenz – mit der Konsequenz des anomalen Transports – sich nicht vermeiden zu lassen. Im Lichte der Unterscheidung zwischen den beiden grundsätzlichen Methoden magnetischen Einschlusses ergibt sich die Frage, ob, und wenn ja, wie sich derartige Instabilitäten und Turbulenz in Tokamaks und Stellaratoren unterscheiden und wodurch sie sich beeinflussen lassen.
Mikroinstabilitäten und anomaler Transport
Wendelstein 7-X [1] (Abb. 1) ist ein Stellarator, für dessen Kraftwerksoptimierung unter anderem folgende Kriterien berücksichtigt wurden: Die magnetohydrodynamische Stabilität des Plasmas bis zu einem für Fusion hinreichend hohen Druck, der gute Einschluss von schnellen Teilchen und die Verringerung des Energieverlustes durch Auswärtstransport von Wärme, wie er durch Stöße der Teilchen untereinander in gekrümmten Magnetfeldern entsteht (neoklassischer Transport) [2]. Mikroinstabilitäten und anomaler Transport waren nicht Teil dieser Optimierung. Sie sind daher Bestandteil derzeitiger Untersuchungen zu Wendelstein 7-X, von denen einige Ergebnisse im folgenden vorgestellt werden .
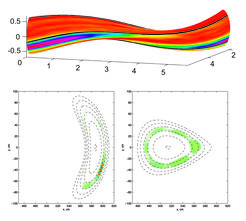
Eine wichtige Instabilität im Plasmakern ist die so genannte ITG-Instabilität (ITG = Ion temperature gradient). Sie wird getrieben durch die radiale Variation der Ionentemperatur und tritt auf, wenn das Verhältnis der typischen Skalenlängen, auf denen Dichte und Temperatur der Ionen variieren, einen Schwellwert überschreitet. Die aus dieser Instabilität sich entwickelnde Turbulenz ist verantwortlich für den anomalen Transport im inneren, heißen Bereich des Plasmas. Abbildung 2 zeigt die Simulation einer solchen Instabilität für Wendelstein 7-X [3]. Bei einer ITG-Instabilität wächst die Störung zeitlich nicht nur an, sondern läuft, da es sich um eine Welle handelt, auch poloidal um den Torus herum. Die kleinskaligen Strukturen, die in Abbildung 2 unten sichtbar sind, rotieren daher zeitlich, ihre Einhüllende bleibt aber unverändert.
Die numerische Lösung der (gyro)kinetischen Gleichung im fünfdimensionalen Phasenraum erfolgte hier mittels einer Teilchenmethode (‚particle-in-cell’). Dabei wird die Bewegung von mehreren Millionen Teilchen in einem äußeren Magnetfeld sowie in dem von ihnen selbst erzeugten elektrischen Feld verfolgt. Die zeitliche Entwicklung des Systems zeigt deutlich, wie eine kleine Anfangsstörung immer weiter anwächst. Da zur Vereinfachung die nichtlinearen Terme in der Gleichung vernachlässigt wurden (Linearisierung), kann das Wachstum der Störung nicht bei einer bestimmten Sättigungsamplitude aufhören und sich Turbulenz ausbilden. Es ist deshalb mit linearen Simulationen nicht möglich, die Stärke des radialen Transports zu berechnen. Allerdings erlaubt der so genannte Mischungswegansatz, zumindest eine Abschätzung dafür anzugeben. Nichtlineare Rechnungen für ITG-Turbulenz sind derzeit selbst unter Einschränkungen nur möglich für einfache Zylindergeometrie und Tokamaks. Für Stellaratorgeometrie sind solche Simulationen noch aufwändiger.
Am Rande des Plasmas werden zusätzlich andere Effekte wichtig: So genannte Driftwellen können durch Stöße der Plasmateilchen untereinander instabil werden. (Die Stöße sind wegen der am Rande niedrigeren Temperatur und der höheren Dichte nicht mehr zu vernachlässigen.) Driftwellen sind eine Folge der radialen Abhängigkeit des Plasmadrucks und laufen senkrecht zu den Feldlinien. Das Plasma kann in diesem Regime durch Zwei-Flüssigkeitsgleichungen beschrieben werden. Sie sind numerisch einfacher zu behandeln als eine kinetische Gleichung, da die Gleichungen – in der unten gezeigten Simulation ein gekoppeltes System von acht partiellen Differentialgleichungen – nur im dreidimensionalen Ortsraum und nicht im fünfdimensionalen Phasenraum gelöst werden müssen. (Eine kinetische Gleichung liefert allerdings eine exaktere Beschreibung des Plasmas.) Im Randbereich ist die typische senkrechte Skalenlänge der Turbulenz so klein, dass eine vollständige Behandlung des Plasmas, selbst bei Einschränkung auf einen kleinen radialen Bereich, numerisch extrem aufwändig wäre. Deshalb wird dort die Näherung eines so genannten Flussschlauches verwendet. Dabei simuliert man nicht das gesamte Plasma; stattdessen ist das Simulationsgebiet in senkrechter Richtung zum Magnetfeld (radial und poloidal) nur ein kleiner lokaler Ausschnitt des Plasmas von typischerweise mehreren Zentimetern Abmessung. Es besitzt aber wegen der oben erwähnten hohen Anisotropie der Turbulenz dennoch eine Länge von vielen Metern entlang der Feldlinien: Das Simulationsgebiet folgt somit den Feldlinien und windet sich mit ihnen um das Plasma herum.
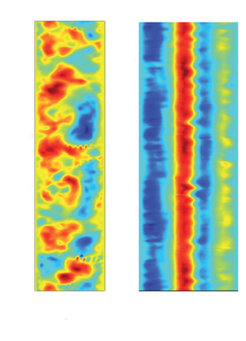
Ein Beispiel für eine solche Turbulenzsimulation zeigt Abbildung 3. Für eine typische Tokamak-Anordnung ist die Turbulenz in der senkrechten Ebene relativ isotrop und gekennzeichnet durch wirbelartige Strukturen mit unterschiedlichen Skalenlängen, die sich zeitlich bilden und wieder auflösen. Sie führen zu einem radialen Transport von Wärme und Teilchen. Verändert man das Profil der Rotationstransformation in einem Tokamak künstlich so, dass es dem eines Stellarators entspricht, dann verringert sich der radiale turbulente Transport deutlich. Die in Abbildung 3 rechts gezeigte Simulation [4] wurde für ein Gleichgewicht von Wendelstein 7-X gerechnet. Der radiale Transport ist dabei gegenüber dem eines Standard-Tokamakgleichgewichts deutlich verringert. Ursache dafür ist die Entstehung starker zonaler Strömungen, die die Turbulenz unterdrücken. Diese Strömungen werden durch die Turbulenz erzeugt, wirken aber – hauptsächlich durch ihre Verscherung – wieder auf diese zurück und verringern sie. In der Abbildung zeigt sich die verbliebene Turbulenz als kleine Strukturierung der vertikalen Streifen, die das elektrische Potenzial der zonalen Strömung repräsentieren.
Ausblick
Das Ziel der Fusionsforschung, zur Lösung des Energieproblems beizutragen, lässt sich sicherer erreichen, wenn das Verhalten von Fusionsplasmen nicht nur in einem einzigen toroidalen Einschlusssystem untersucht wird: Die Erforschung von Instabilitäten und Turbulenz in Stellaratoren bietet im Vergleich zu Tokamak-Konfigurationen eine neue Sichtweise in Hinblick auf den anomalen Transport.
Künftige Turbulenzuntersuchungen in Stellaratoren werden durch zwei komplementäre Aspekte bestimmt sein: Einerseits wird es eine Reihe kleinerer Stellaratorexperimente – zum Beispiel TJ-II in Spanien sowie HSX (Helical Stellarator Experiment) in den USA – bis mittelgroßer Anlagen geben – LHD (Large Helical Device) in Japan, NCSX (National Compact Stellarator Experiment) in den USA sowie Wendelstein 7-X, die deutlich unterschiedliche Magnetfeldstrukturen im Konfigurationsraum der Stellaratoren untersuchen. Andererseits wird das rasche Wachstum von Computerressourcen die Untersuchung immer vollständigerer physikalischer Modelle zulassen. Somit besteht begründete Hoffnung, durch detaillierte Experimentanalyse und „computational turbulence“ zu einem grundlegendem Verständnis zu kommen, das für die Realisierung der Kernfusion wesentlich ist. (R. Kleiber, R. Hatzky, G. Jost, V. Kornilov, J. Nührenberg, B. Scott, L. Villard)


