Forschungsbericht 2017 - Max-Planck-Institut für Chemische Physik fester Stoffe
Elektronische Quantenmusik
Jedes Musikinstrument besitzt eine eigene Klangfarbe. Wenn die gleiche Note auf verschiedenen Instrumenten gespielt wird, unterscheidet sich der Klang durch Beiträge von Obertönen, also Tönen mit dem Vielfachen der Grundfrequenz. Die charakteristische Klangfarbe ist demnach durch das Frequenzspektrum gegeben. So erzeugt zum Beispiel eine Flöte hauptsächlich gerade Obertöne und klingt hell und klar, wogegen die Oboe eher ungerade Obertöne produziert und viel weicher klingt.
Analog zu Musikinstrumenten hat jedes Metall auch ein eigenes Frequenzspektrum, ähnlich einem charakteristischen Akkord. Wird die Saite einer Geige mit dem Bogen gestrichen, fängt sie an zu vibrieren, sie oszilliert mit der Zeit und bringt die Luft im Klangkörper zum Schwingen. Im Metall wird durch ein sich änderndes Magnetfeld eine Schwingung einer Messgröße, wie etwa die Magnetisierung oder Leitfähigkeit, angeregt.
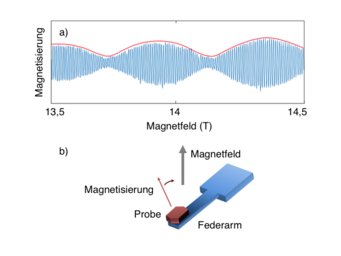
Abbildung 1a zeigt als Beispiel die oszillierende Magnetisierung eines Metalls als Funktion der Stärke eines äußeren Magnetfeldes. In diesem Fall spielt das Magnetfeld die Rolle der Zeit. Diese Oszillationen spiegeln die Quantisierung der Elektronenwellenfunktion wider und werden deshalb Quantenoszillationen genannt. Bei jeder Schwingung bewegt sich ein quantisiertes Energieniveau durch das chemische Potenzial und erzeugt eine vorübergehende Erhöhung der Messgröße. Für jede Magnetfeldrichtung in Bezug zur Kristallstruktur eines Metalls gibt es ein charakteristisches Spektrum, einen Quantensound. Bei Musikinstrumenten verursacht die jeweilige Form des Instruments das typische Frequenzspektrum. Ähnlich entspricht in Metallen das Frequenzspektrum einer gekrümmten Fläche im Raum. Diese sogenannte Fermifläche ist wie der Klangkörper der Elektronen..
Elektronen sind in Metallen für den elektrischen Strom verantwortlich. Sie bewegen sich jedoch nicht wie ein Wasserstrom, sondern stoßen in normalen Metallen so oft an die Atomrümpfe, dass sie sofort aufhören zu fließen, sobald die treibende Kraft, also die Spannung, nicht mehr anliegt. Wäre der Strom hydrodynamisch, also mit genügend Trägheit versehen, würde er mit Schwung ein bisschen weiterfließen. Dazu müssten die bremsenden Stoßprozesse deutlich schwächer ausgeprägt sein. Eine grundlegende Frage ist, ob es auch einen hydrodynamischen Stromfluss bei Elektronen gibt.
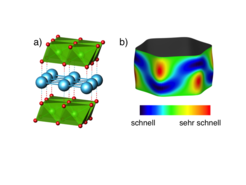
In sogenannten Delafossiten wurden nun zum ersten Mal Hinweise auf einen solchen hydrodynamischen elektronischen Transport gefunden [1]. Delafossit-Metalle haben eine hexagonale Struktur, in der sich extrem gut leitende Atomschichten etwa aus Palladium oder Platin mit fast isolierenden Oxidschichten abwechseln (Abbildung 2a). In den leitenden Schichten verhalten sich die Elektronen fast frei wie in einem Gas. In den Oxidschichten jedoch erfahren sie starke Wechselwirkungen mit anderen Elektronen. Deshalb ist die Leitfähigkeit senkrecht zu den Ebenen viel kleiner als innerhalb der Ebenen. Für einen solchen Fall ist die Fermifläche zylindrisch (Abbildung 2b).
Schafft man es, die Quantenmusik der Elektronen zu erlauschen, kann man dem Metall die Geheimnisse des Elektronentransports entlocken. Unterschiedliche Klänge bedeuten unterschiedliche elektrische Eigenschaften. So kann man zum Beispiel folgende Fragen beantworten. Welche Wechselwirkungen sind in dem Metall wichtig und in welcher Richtung? Wie gut kann der Strom in den verschiedenen Kristallrichtungen fließen? Welchen Einfluss haben Verunreinigungen im Kristallgitter?
Es ist jedoch eine technische Herausforderung, den Quantensound von Elektronen zu hören. Nur bei sehr tiefen Temperaturen von unter einem Kelvin (-272° C), in starken Magnetfeldern von ungefähr 10 T (mehr als in einem Magnetresonanzspektrographen) und in sehr reinen Metallen ertönt die Elektronenmusik. Und selbst dann ist sie so leise, dass Störsignale beim Messen sie regelrecht überdecken, wie ein lautes Rauschen die Musik übertönt. Damit wir sie trotzdem hören können, wurde der gleiche Trick wie bei einer E-Gitarre angewandt: Die Schwingungen der Saite sind ohne Verstärker so leise, dass man sie bei Zimmerlautstärke kaum hören kann. Werden sie aber verstärkt, erzeugt der Lautsprecher einen hörbaren Ton.
In unserem Labor wurde ganz analog in einem neuen Aufbau ein sehr empfindlicher Tieftemperaturverstärker in den Millikelvin-Kühlschrank eingebaut, um die Quantenoszillationen bei tiefen Temperaturen so zu verstärken, dass das Level der Oszillationen über dem der Störsignale liegt. Das Schwierige war, im äußeren Magnetfeld die Störsignale am Eingang des Verstärkers weit genug zu unterdrücken, um den Verstärker in Feldern bis zu 15 T zu benutzen und die Quantenoszillationen des Delafossit-Metalls PdRhO2 mit hoher Auflösung zu messen [2, 3].
Wie die Schwingungen detektiert wurden, zeigt Abbildung 1b. Die Elektronen im Metall reagieren auf das äußere Magnetfeld, indem sie Kreisbahnen beschreiben. Dies wiederum führt zu einer Magnetisierung der Metallprobe: Sie wird zur Kompassnadel. Die Probe will sich daher nach dem angelegten Magnetfeld ausrichten und übt eine Kraft auf einen winzigen Federarm aus. Das resultierende Drehmoment wird gemessen und oszilliert mit der Magnetisierung im Magnetfeld.
Die so gemessenen Quantenoszillationen von PdRhO2 zeigt Abbildung 1a. Sie bestehen aus zwei Frequenzen, die sehr nah beieinander liegen, also leicht verstimmt sind. Die Verstimmung ist so klein, dass man nicht zwei verschiedene Töne wahrnimmt, sondern Schwebungen auftreten. In der Akustik hört man in dem Fall einen Ton, der „wummert“, also periodisch laut und leise wird. Die Verstimmung als Abhängigkeit der Magnetfeldrichtung zeigt uns, dass dieses Material eine erstaunlich zweidimensionale Elektronenleitung besitzt, wobei die Verstimmung die Abweichung von der Zweidimensionalität widerspiegelt: Der Fermizylinder hat kleine Hügel (Abbildung 2b). Unsere Messung zeigt daher, dass die Leitfähigkeit in der Ebene, gemessen an der senkrecht dazu, besser als erwartet ist. Die Elektronen sind besonders schnell, da die bremsende Wechselwirkung mit den Oxidschichten kleiner als gedacht ist.
Es bleibt nun herauszufinden, warum genau in diesen Metallen hydrodynamischer Transport stattzufinden scheint. Dafür werden noch andere Verbindungen der gleichen Klasse untersucht. Der Quantensound eines jeden Metalls ist unterschiedlich, er gibt uns ein sehr präzises Verständnis der Elektronen und deren Wechselwirkungen im Metall. Wenn wir genau genug zuhören, können wir so der Natur - Ton für Ton - ihre Geheimnisse ablauschen.