Forschungsbericht 2017 - Max-Planck-Institut für Hirnforschung
Informationscodierung mit neuronalen Spikes
Einleitung
Um zu verstehen, wie das Gehirn kognitive Funktionen implementiert, müssen wir mehr darüber wissen, wie neurale Aktivität Information kodiert. Die neurale Kommunikation beruht hauptsächlich auf kurzen, elektrische Impulsen, sogenannten Spikes (Aktionspotenziale). Ein Spike Train kann als Serie von Nullen und Einsen verstanden werden, wobei „1“ für das Vorhandensein und „0“ für die Abwesenheit eines Spikes steht. Wissen über den Zusammenhang zwischen Spike-Zeiten und neuraler Informationsübertragung zu erlangen ist nicht einfach. Zum einen besteht die Hürde, die relevanten Kodierungsmerkmale genau zu bestimmen. Ist die Gesamtzahl der Spikes von Bedeutung, oder nur deren Auftreten in einem spezifischen Muster, wie Spike-doublets oder – triplets? Die Forschungsgruppe hat sich das Ziel gesetzt, die minimal nötigen Merkmale zu bestimmen, die für die Kodierung neuraler Information verantwortlich sind.
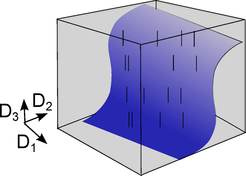
Abb. 1: Ein niedrig dimensionaler Unterraum genügt zur Informationsbestimmung. Für viele Situationen ist es ausreichend, nur den Raum der paarweisen Korrelationen auszuwerten (hier schematisch in blau dargestellt), um die neuronale Information zu verstehen, anstatt den Raum aller möglichen Spike-Kombinationen (grau, Raumdimensionen D1-D3) betrachten zu müssen.
Das häufig verwendete Paradigma rate coding nimmt an, dass die Anzahl der Spikes pro Zeiteinheit die einzige informationstragende Variable ist. Jedoch gibt es zunehmend eine Evidenz dafür, dass Neuronen Reizmerkmale kodieren, indem die temporale Struktur der Spike Trains verändert wird, ohne dass die Feuerrate selbst geändert wird. Dies könnte darauf zurückzuführen sein, dass der temporale Code einen höheren Informationsgehalt hat als der Raten-Code. Um das zu überprüfen, entwickelten die Forscher eine Fourier-basierte Methode, um den gesamten neuralen Informationsgehalt quantitativ zu erfassen. Mit dieser Methode zeigte sich, dass paarweise Spike-Korrelationen den Informationsgehalt vollständig bestimmen. Die Untersuchung des Informationsgehaltes und dessen Komponenten ergab, dass die Verbesserung des Signal-Rausch-Verhältnisses bei zuverlässigen Neuronen den Informationsgehalt mehr steigert als bei stark verrauschten Neuronen. Da paarweise Korrelationen einfacher zu messen sind, ermöglichen die Ergebnisse bei zukünftigen Forschungen an neuralen Informationen mehr Robustheit und einfachere Analyse (Abb. 1). Die Erkenntnis dieser Arbeit deutet in Hinblick auf zukünftige Forschungsgebiete an, dass paarweise Spike-Korrelationen einen zentralen Stellenwert zur Bestimmung neuraler Informationen einnehmen werden.
Der Einfluss linearer Faktoren auf den neuralen Code
Phänomene im Gehirn basieren nicht nur auf linearen Filtern, sondern auf komplexen, nicht-linearen Wechselwirkungen und Rückkopplungen. In den vergangenen Jahrzehnten wurden zahlreiche mathematische Methoden aus der Physik angewandt, um solche Systeme besser zu verstehen. Eine davon ist das Konzept der linearen Antwortfunktion. Zu verstehen, wie lineare und nicht lineare Effekte wechselwirken und in Modellen angemessen kombiniert werden können, bleibt eine große Herausforderung.
Jüngste Arbeiten der Max-Planck-Forschergruppe zeigen die Anwendungsgebiete und -grenzen linearer Antwortfunktionen in der Neurowissenschaft auf. Um ein tieferes Verständnis zu erlangen, wie die Aktivität neuraler Schaltkreise mit deren Funktionalität zusammenhängt, werden Modellansätze verwendet, die auf linearen Antwortfunktionen beruhen. Diese Modellansätze ermöglichen einen Einblick in bedeutende Bereiche der Neurowissenschaft wie Ratendynamik, Synchronität, globale Oszillationen und Informationstheorie.
Wenn ein Reiz die Feuerrate der Neuronen moduliert, ist es oft möglich, die Ratendynamik mathematisch durch eine mathematische Faltung des Reizes mit einer linearen Antwortfunktion zu beschreiben (Abb. 2). Diese oft verwendetet Methode hat auch bei Neuronenpaaren Anwendung gefunden. Wird der Stimulationsreiz mit einer linearen Antwortfunktion kombiniert, kann die daraus entstehende paarweise Korrelation zur Beschreibung von sowohl Neuronenpaaren als auch allgemein von Phänomenen der Netzwerkkorrelation verwendet werden.

Abb. 2: Durch einen Stimulus (rote Linie) werden in Neuronen-Populationen Spike-Antworten erzeugt (dünne vertikale Linien). Im Rahmen der linearen Antworttheorie entspricht die aufsummierte Antwort aller Neuronen (breite vertikale Balken) einer frequenzgefilterten Version des Stimulus.
Eine weitere Anwendung linearer Antwortfunktionen in der Neurowissenschaft ist die Vorhersage sogenannter Synchronisationsübergänge, die beschreiben, wann ein irregulär aktives Netzwerk einen globalen Rhythmus annimmt. Es wird angenommen, dass der globale Rhythmus für viele kognitive Funktionen, wie Aufmerksamkeit und den damit zusammenhängenden Phänomenen, von großer Bedeutung ist. Zu wissen, wann rhythmische Aktivität in Netzwerken auftritt und wann nicht, ist demzufolge für das Verständnis der Hirnfunktion essentiell. Der Beitrag der linearen Antwortfunktionen ist in diesem Bereich von besonderer Bedeutung: sie ermöglichten die Konstruktion einer Antwortmatrix, deren Eigenwerte direkt vorhersagen, ob der Übergangspunkt zum globalen Rhythmus in einem Netzwerk existieren kann. Dies erlaubt es, das Verhalten neuraler Netzwerke auf Grund von synaptischen und neuronalen Eigenschaften ohne Simulationen direkt vorherzusagen.
Zusammenfassend lässt sich sagen, dass die lineare Antwortfunktion mittlerweile als besonders nützliche und vielseitige Methode anerkannt ist. Neueste Arbeiten zeigten jedoch, dass neue theoretische Konzepte benötigt werden, um ein tieferes Verständnis in der theoretischen Neurowissenschaft zu erlangen. Zudem bestehen weiterhin große Herausforderungen in der Entwicklung von Theorien über neurale Netzwerke. Dazu gehören die Hinzunahme von Feedbackschleifen und die nichtstationäre Dynamik, die experimentell in neuralen Netzwerken beobachtet werden.

