Forschungsbericht 2016 - Max-Planck-Institut für Mikrostrukturphysik
Was fallende Katzen für die Dichtefunktionaltheorie bedeuten
Katzen verfügen über die erstaunliche Fähigkeit, selbst dann auf ihren Pfoten zu landen, wenn sie bei einem Drehimpuls von Null mit den Beinen nach oben fallen gelassen werden. Diese Meisterleistung an Katzenagilität scheint dem Grundprinzip der Drehimpulserhaltung zu widersprechen: Wenn die Katze keinen Drehimpuls hat, wie kann sie sich dann drehen? Der Trick besteht darin, dass die Katze kein starrer Körper ist und deshalb durch Verdrehen ihres Körpers eine Netto-Rotation erreichen kann, wie in Abbildung 1 dargestellt. Mathematisch betrachtet trassiert die Sequenz von Verdrehungen eine geschlossene Bahn im Raum aller möglichen Formen, die die Katze annehmen kann [1].

Die Vorstellung, dass eine Winkelvariable eine Verschiebung erfahren kann, wenn ein Teilsystem um eine geschlossene Bahn herumgeführt wird, ist die Essenz der Berry-Phase [2], eines quantenmechanischen Effekts analog zur fallenden Katze. Erfährt beispielsweise ein Molekül eine zyklische Verformung, kann die elektronische Wellenfunktion eine Phasenverschiebung erfahren, die als molekulare geometrische Phase bezeichnet wird [3]. Diese molekulare geometrische Phase wurde ursprünglich unter der Annahme definiert, dass sich die Elektronen instantan an Verschiebungen der Kerne anpassen, der sogenannten Born-Oppenheimer(BO)-Näherung. Aktuelle Forschungen am Max-Planck-Institut für Mikrostrukturphysik haben gezeigt, wie sich eine exakte molekulare geometrische Phase [4, 5] ohne Bezugnahme auf die BO-Näherung definieren lässt. Diese Definition verwendet das Konzept einer exakten Faktorisierung der Elektron-Kern-Wellenfunktion [6, 7] und ermöglicht die Einführung einer Dichtefunktionaltheorie (DFT) für das Gesamtsystem von Elektronen und Kernen, die vollkommen unabhängig von der BO-Näherung ist [8].
Für die gekoppelte Elektron-Kern-Dynamik, die heute aufgrund ihrer bedeutenden Rolle in chemischen und physikalischen Prozessen großes Interesse genießt, eröffnet sich damit ein grundlegend neuer Weg zur Beschreibung nicht adiabatischer Effekte.
Grundlagen der Dichtefunktionaltheorie
Die DFT zählt unzweifelhaft zu den erfolgreichsten Theorien der Wissenschaft und wird jedes Jahr in Zehntausenden Veröffentlichungen verwendet. Die DFT ist eine in sich abgeschlossene Theorie wechselwirkender Elektronen, die allein mit der Elektronendichte als Funktion von drei räumlichen Koordinaten auskommt, wodurch die zeitaufwendige Berechnung der exponentiell komplexen Vielelektronen-Wellenfunktion entfällt. Ein von Hohenberg und Kohn 1964 bewiesenes Theorem [9] besagt, dass wir zur Ermittlung der Grundzustandsdichte nur die Energie, ausgedrückt als Funktional der Dichte, minimieren müssen. Die sich minimierende Dichte kann durch Lösen einer Einteilchen-Schrödinger-Gleichung und durch Addition der Beiträge |ψn(r)|2 aller besetzten Zustände sehr effizient berechnet werden. Faktisch wurde das ursprüngliche System wechselwirkender Elektronen durch ein Hilfssystem nicht-wechselwirkender Elektronen ersetzt, die ein als Kohn-Sham-Potenzial bezeichnetes Mean-Field-Potenzial spüren [10]. Da das Kohn-Sham-Potenzial ein Funktional der – noch zu bestimmenden – Dichte ist, muss die Lösung selbstkonsistent gefunden werden.
Die praktischen Grenzen der DFT, die sich aus der Notwendigkeit ergeben, das effektive Potenzial nähern zu müssen, wurden umfassend dokumentiert. Weniger bekannt ist dagegen eine signifikante konzeptionelle Beschränkung in dem Sinne, dass es sich zwar um eine exakte Theorie für Elektronen handelt, die sich im Potenzial statischer Kerne bewegen, nicht aber um eine exakte Theorie für Elektronen und Kerne. Tatsächlich geht das Hohenberg-Kohn-Theorem davon aus, dass die Kerne feste Punktladungen sind, während sie sich in Wirklichkeit bewegen, vibrieren und den Gesetzen der Quantenmechanik unterliegen. Der Erfolg der DFT ist deshalb von der Genauigkeit der Born-Oppenheimer-Näherung abhängig – der Annahme also, dass sich die Elektronen, weil sie viel leichter als die Kerne sind, schneller bewegen und praktisch instantan auf die Kernbewegung reagieren können. Die Kerne werden also effektiv als statische Punktladungen betrachtet – genau die Voraussetzung, von der das Hohenberg-Kohn-Theorem ausgeht. Dies ist die sogenannte adiabatische Näherung: Wir erhalten, wie oben beschrieben, für jeden festen Satz von Kernpositionen eine andere elektronische Energie. Diese elektronische Energie als Funktion der Kernpositionen definiert zusammen mit der Coulomb-Abstoßung der Kerne eine adiabatische „Potenzialenergiefläche“. Die Kernbewegung findet auf dieser Potenzialenergiefläche statt.
Die BO-Näherung ist normalerweise eine gute Näherung für den Grundzustand, versagt aber, wenn sich eine Potenzialenergiefläche im angeregten Zustand der Potenzialenergiefläche im Grundzustand zu stark nähert, wie es bei konischen Durchschneidungen geschieht, wo sich die beiden Flächen tatsächlich schneiden. Die Regionen, in denen die BO-Näherung versagt, sind genau die, „in denen interessante Dinge passieren“. Sie werden deshalb in Physik und Chemie intensiv erforscht. Leider hat die Standard-DFT gravierende Grenzen, wenn es um die Beschreibung solcher Situationen geht. Um erläutern zu können, wie wir eine über die BO-Näherung hinausgehende DFT definiert haben, müssen wir zunächst kurz das Konzept der molekularen geometrischen Phase einführen.
Geometrische Phase
Geometrische Phasen haben in der Physik breite Anwendung gefunden und sind ein wichtiges Element der Mathematik topologischer Bandstrukturen. Wie oben beschrieben, erwirbt ein Quantenzustand, der im Konfigurationsraum entlang einer zyklischen Bahn geführt wird, eine Phasenverschiebung eiy, die nur von der Bahngeometrie abhängt. In der Essenz ist γ ein dimensionsloses Maß der von der Bahn eingeschlossenen Fläche. In Abbildung 2 sind zwei prototypische Beispiele für geometrische Phasen zu sehen. Abbildung 2(a) veranschaulicht die geometrische Phase eines Spin-1/2-Teilchens, während die Abbildungen 2(b) und 2(c) die molekulare geometrische Phase zeigen, wie sie sich in dreiatomigen Molekülen manifestiert.
![Abb. 2: Beispiele für Berry-Phasen. (a) Die adiabatische Berry-Phase eines Spin-1/2-Teilchens entspricht -1/2-mal dem von der Bahn (grüne Kurve) eingeschlossenen Raumwinkel Ω, die durch ein sich langsam veränderndes Magnetfeld bestimmt wird [2]. (b) In einem dreiatomigen Molekül wie Na3 ist die molekulare Berry-Phase eine Folge der konischen Durchschneidung in der gleichseitigen Geometrie. (c) Die Verschiebungen der Kerne (Pfeile) werden an einer Reihe von Punkten entlang der ersten Hälfte einer zyklischen Bahn dargestellt, die die konische Durchschneidung umschließt. Die elektronischen BO-Wellenfunktionen, ψe und ψe‘,verändern ihr Vorzeichen, weil sich ihre Knoten (gestrichelte Linien) nur um π drehen, während die Kerne einen kompletten Zyklus von 2π durchlaufen.](/11635906/original-1508158517.jpg?t=eyJ3aWR0aCI6MjQ2LCJvYmpfaWQiOjExNjM1OTA2fQ%3D%3D--80d175a3e8f888a8285814492b1dbe471d6a13a5)
Wenn sich die Kerne eines dreiatomigen Moleküls entlang einer geschlossenen Bahn bewegen, die eine konische Durchschneidung umschließt, ändert die elektronische BO-Wellenfunktion ihr Vorzeichen [3], wie in Abbildung 2 zu sehen ist. Dieser Vorzeichenwechsel entspricht einer Phase γ = π und ist deshalb ein spezieller Fall einer Berry-Phase; dabei handelt es sich faktisch um eine topologische Invariante, da sie unempfindlich gegenüber Bahnverformungen ist. Wenn man eine Reihe von Schritten entlang der ersten Hälfte der zyklischen Bahn verfolgt (Abb. 2(c)), kann man den Vorzeichenwechsel veranschaulichen. Die beiden relevanten elektronischen BO-Zustände ändern ihr Vorzeichen, da ihre Knoten mit der Hälfte der Geschwindigkeit der gemeinsamen Kern-(Pseudo)-Rotation rotieren. Dieses Verhalten impliziert eine starke Kopplung zwischen Elektronen und Vibrationen und hat dramatische Auswirkungen auf die Energieniveaus des Moleküls. Das lässt sich in der Schwingungsspektroskopie beobachten.
Exakte Faktorisierung der Elektron-Kern-Wellenfunktion
In Bezug auf die oben beschriebene molekulare geometrische Phase gibt es allerdings eine Unzulänglichkeit: Sie hängt entscheidend vom singulären Verhalten der elektronischen BO-Wellenfunktionen an der konischen Durchschneidung ab. Aber das ist genau die Stelle, an der die BO-Näherung versagt. Da die traditionelle Definition der geometrischen Phase die BO-Näherung beinhaltet, stellt sich die Frage, was mit der geometrischen Phase geschehen würde, wenn man eine exakte Berechnung durchführen könnte.
Diese Frage wurde in einem molekularen Modellsystem untersucht, das eine konische Durchschneidung und somit eine geometrische Phase von π in der BO-Näherung aufweist [4]. Die Berechnungen basierten auf der sogenannten exakten Faktorisierung, bei der die volle Elektron-Kern-Wellenfunktion als Produkt einer reinen Kern-Wellenfunktion und einer elektronischen Wellenfunktion geschrieben wird [6, 7]. Letztere hängt auch von den Kernkoordinaten ab und ihr Betragsquadrat hat die Bedeutung einer bedingten Wahrscheinlichkeitsdichte. Es stellt sich heraus, dass sich die singuläre konische Durchschneidung der adiabatischen Potenzialenergieflächen in der exakten Berechnung in eine Durchkreuzung von glatten „diabatischen“ Potenzialenergieflächen wandelt, wodurch sich die molekulare geometrische Phase von π auf 0 verändert. Die Schlussfolgerung daraus ist, dass – in diesem Fall – die adiabatische molekulare geometrische Phase ein Artefakt der BO-Näherung ist. Die Frage, ob die exakte molekulae rgeometrische Phase jemals ungleich Null ist, blieb dabei offen.
Eine exakte molekulare geometrische Phase, die nicht verschwindet [5], wurde in einem dreiatomigen Molekülmodell gefunden, das dem ursprünglichen Beispiel in Abbildung 2(c) nahe kommt. Das Modell hat ebenfalls eine konische Durchschneidung und eine adiabatische geometrische Phase von π, weist aber im Gegensatz zu Ref. [4] einen entarteten Grundzustand auf. Diese Entartung eröffnet eine neue Möglichkeit – nämlich, dass es sich bei der molekularen Berry-Phase um eine geometrische Größe statt um eine topologische Invariante handelt. Der Unterschied lässt sich am besten durch die grafische Darstellung der Berry-Krümmung nachvollziehen, die wie folgt definiert werden kann. Mithilfe des Stokes’schen Integralsatzes kann die molekulare geometrische Phase – das Kurvenintegral eines effektiven Vektorpotenzials – in das Flächenintegral der sogenannten Berry-Krümmung umgewandelt werden, die demzufolge ein effektives Magnetfeld repräsentiert. Abbildung 3 zeigt die Berry-Krümmung des dreiatomigen Molekülmodells als Funktion der beiden Normalmoden-Koordinaten der relevanten Vibrationsmoden. Jetzt lässt sich der Unterschied zwischen der exakten Berechnung und der BO-Näherung leicht identifizieren: Die Berry-Krümmung ist in der exakten Berechnung eine glatte Funktion, während sie in der BO-Näherung singulär wird [5].
Dichtefunktionaltheorie ohne Born-Oppenheimer Näherung
Als glatte Funktion der Kern-Koordinaten statt einer Singularität kann die exakte Berry-Krümmung durch variationelle Optimierung eines Funktionals auf die gleiche Weise berechnet werden, wie die berühmte Brachistochrone-Kurve, die von den Bernoulli Brüdern 1696 untersucht wurde, durch Minimierung des Funktionals gefunden werden kann, dessen Wert die Zeit angibt, die eine Murmel benötigt, um auf einer gebogenen Rampe von einem Fixpunkt zu einem anderen herabzugleiten.
Mithilfe der Methode der exakten Faktorisierung ist es möglich, ein Funktional zu definieren, das von der Elektronendichte und dem sogenannten quantengeometrischen Tensor abhängt – eine Größe, die die Berry-Krümmung, aber auch noch weitere Informationen enthält [8]. Das Funktional gibt den Wert der Grundzustandsenergie an und kann durch Lösung eines Systems aus drei gekoppelten Gleichungen minimiert werden, nämlich (i) Kohn-Sham-Gleichungen mit einem effektiven Potenzial, das ein Funktional der Dichte und des quantengeometrischen Tensors ist; (ii) Euler-Lagrange Gleichungen, die den quantengeometrischen Tensor ermitteln, und (iii) die Schrödinger-Gleichung der Kerne.
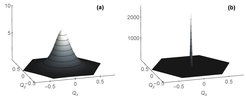
![Abb. 4: Elektronendichte eines dreiatomigen Moleküls. Die konditionale Elektronendichte, 2n3-n1-n2, deren Wert durch die Höhenlinien angegeben wird, ist als Funktion von Qx und Qy dargestellt, die in Abbildung 2(c) definiert werden; ni ist die Besetzung des Valenzorbitals von Atom i. (a) Die konditionale Elektronendichte ist in der auf exakter Faktorisierung basierenden DFT eine glatte Funktion von Qx und Qy [8]. (b) Die konditionale Elektronendichte hat in der auf Born-Oppenheimer basierenden Standard-DFT eine artifizielle Singularität in der konischen Durchschneidung, wobei sich die Elektronendichte selbst für infinitesimale Kernverschiebungen um einen endlichen Wert ändert. Dieses unphysikalische Verhalten, das bei standardmäßigen Grundzustands-DFT-Berechnungen auftritt, wird in der DFT mit exakter Faktorisierung korrigiert.](/11635700/original-1508158508.jpg?t=eyJ3aWR0aCI6MjQ2LCJvYmpfaWQiOjExNjM1NzAwfQ%3D%3D--0b6eeaa08bcb88084d65da3610d6cab72e5e194e)
Diese Gleichungen behalten die enorm erfolgreiche Mean-Field-Struktur der DFT für den elektronischen Teil des Problems bei, während sie eine exakte Beschreibung der Quantenkernbewegung und der nicht-adiabatischen Kopplung zwischen Elektronen und Kernen liefern. Auf diese Weise überwindet die Theorie die Beschränkungen der BO-Näherung in der konventionellen DFT. Eine Anwendung der Theorie auf das oben genannte dreiatomige Modell wird in Abbildung 4 dargestellt. Es bleibt als Herausforderung für die Zukunft, akkurate funktionale Näherungen für das Kohn-Sham-Potenzial herzuleiten und dabei die funktionale Abhängigkeit von der Berry-Krümmung in die bekannten Funktionale der DFT einzubauen.
Literaturhinweise
in Dynamics and Control of Mechanical Systems; M. Enos (ed.)
Fields Institute Communications 1, 193-218, AMS, 1993

![Abb. 2: Beispiele für Berry-Phasen. (a) Die adiabatische Berry-Phase eines Spin-1/2-Teilchens entspricht -1/2-mal dem von der Bahn (grüne Kurve) eingeschlossenen Raumwinkel Ω, die durch ein sich langsam veränderndes Magnetfeld bestimmt wird [2]. (b) In einem dreiatomigen Molekül wie Na3 ist die molekulare Berry-Phase eine Folge der konischen Durchschneidung in der gleichseitigen Geometrie. (c) Die Verschiebungen der Kerne (Pfeile) werden an einer Reihe von Punkten entlang der ersten Hälfte einer zyklischen Bahn dargestellt, die die konische Durchschneidung umschließt. Die elektronischen BO-Wellenfunktionen, ψe und ψe‘,verändern ihr Vorzeichen, weil sich ihre Knoten (gestrichelte Linien) nur um π drehen, während die Kerne einen kompletten Zyklus von 2π durchlaufen. Abb. 2: Beispiele für Berry-Phasen. (a) Die adiabatische Berry-Phase eines Spin-1/2-Teilchens entspricht -1/2-mal dem von der Bahn (grüne Kurve) eingeschlossenen Raumwinkel Ω, die durch ein sich langsam veränderndes Magnetfeld bestimmt wird [2]. (b) In einem dreiatomigen Molekül wie Na3 ist die molekulare Berry-Phase eine Folge der konischen Durchschneidung in der gleichseitigen Geometrie. (c) Die Verschiebungen der Kerne (Pfeile) werden an einer Reihe von Punkten entlang der ersten Hälfte einer zyklischen Bahn dargestellt, die die konische Durchschneidung umschließt. Die elektronischen BO-Wellenfunktionen, ψe und ψe‘,verändern ihr Vorzeichen, weil sich ihre Knoten (gestrichelte Linien) nur um π drehen, während die Kerne einen kompletten Zyklus von 2π durchlaufen.](/11635906/original-1508158517.jpg?t=eyJ3aWR0aCI6MzQxLCJmaWxlX2V4dGVuc2lvbiI6ImpwZyIsIm9ial9pZCI6MTE2MzU5MDZ9--69f556869e3eda79eb4e82f9262013914dbe6d73)

![Abb. 4: Elektronendichte eines dreiatomigen Moleküls. Die konditionale Elektronendichte, 2n3-n1-n2, deren Wert durch die Höhenlinien angegeben wird, ist als Funktion von Qx und Qy dargestellt, die in Abbildung 2(c) definiert werden; ni ist die Besetzung des Valenzorbitals von Atom i. (a) Die konditionale Elektronendichte ist in der auf exakter Faktorisierung basierenden DFT eine glatte Funktion von Qx und Qy [8]. (b) Die konditionale Elektronendichte hat in der auf Born-Oppenheimer basierenden Standard-DFT eine artifizielle Singularität in der konischen Durchschneidung, wobei sich die Elektronendichte selbst für infinitesimale Kernverschiebungen um einen endlichen Wert ändert. Dieses unphysikalische Verhalten, das bei standardmäßigen Grundzustands-DFT-Berechnungen auftritt, wird in der DFT mit exakter Faktorisierung korrigiert. Abb. 4: Elektronendichte eines dreiatomigen Moleküls. Die konditionale Elektronendichte, 2n3-n1-n2, deren Wert durch die Höhenlinien angegeben wird, ist als Funktion von Qx und Qy dargestellt, die in Abbildung 2(c) definiert werden; ni ist die Besetzung des Valenzorbitals von Atom i. (a) Die konditionale Elektronendichte ist in der auf exakter Faktorisierung basierenden DFT eine glatte Funktion von Qx und Qy [8]. (b) Die konditionale Elektronendichte hat in der auf Born-Oppenheimer basierenden Standard-DFT eine artifizielle Singularität in der konischen Durchschneidung, wobei sich die Elektronendichte selbst für infinitesimale Kernverschiebungen um einen endlichen Wert ändert. Dieses unphysikalische Verhalten, das bei standardmäßigen Grundzustands-DFT-Berechnungen auftritt, wird in der DFT mit exakter Faktorisierung korrigiert.](/11635700/original-1508158508.jpg?t=eyJ3aWR0aCI6MzQxLCJmaWxlX2V4dGVuc2lvbiI6ImpwZyIsIm9ial9pZCI6MTE2MzU3MDB9--4aca86834c9239e985555f7b55511b194b5ea21d)